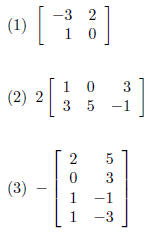The Gauss Jordan method allows us to isolate the
coefficients of a system of
linear equations making it simpler to solve for.
Creating the Augmented Matrix
To isolate the coefficients of a system of linear equations we create an
augmented
matrix as follows:

Exercise Represent the following systems of linear
equations by an augmented
matrix:
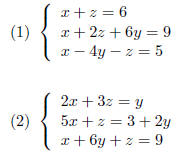
Exercise Construct the system of linear equations
from the augmented matricies
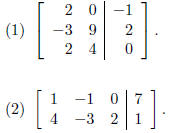
Row Operations
We can manipulate an augmented matrix using the following rules :
(1) Switch any two rows .
(2) Multiply a row by a nonzero real number.
(3) Adding a nonzero multiple of one row to any other row.
Exercise Rewrite the given augmented matrix
according to the row operations
specified.
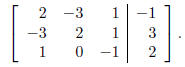
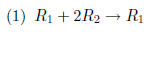
(2) Switch first and second row, and
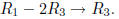
Gauss Jordan Method
(1) Write system of equations so that variables are on the right side of the
equals sign .
(2) Write the augmented matrix for the system of equations
(3) Use the row operations to rewrite the augmented matrix so that the first
row looks like :
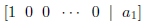
(3) Use the row operations to rewrite the augmented matrix
so that the second
row looks like:
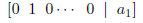
(4) Continue this process for as long as you can.
Example Solve the following system of linear
equations using the Gauss Jordan
method.
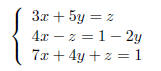
Check Your Answers !!!
Insert the values that you calculated for x, y and z to check that the system of
linear euqations hold.
Solving a system of equations with an infinite number
of solutions
Example Solve the following system of linear equations
using the Gauss Jordan
method.

Solution:
What does this mean?
Addition and Subtraction of Matricies
Definition We say that the following matrix is an n × m
matrix
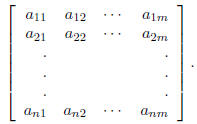
Describe the following matrices.

Definiton Two matricies are equal if they are of
the same size and have similar
coresponding elements.
Example Do there exist values that make the
following matricies equal? If so,
what are the values? If not, why not?
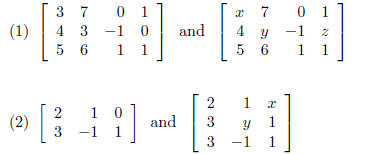
Adding Matrices
To add two matricies which have the same size you do the following operation

YOU CAN ONLY ADD MATRICES OF THE SAME SIZE!
Notation:
If
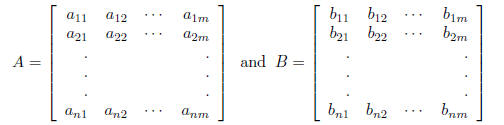
then
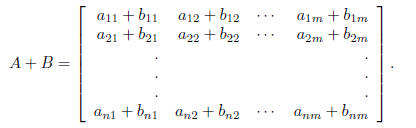
Multiplying a matrix by a constant: If A is the matrix
above and k is a
constant then
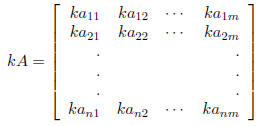
Subtracting Matrices
Let A and B be the matrices describes above, then
A − B = A + (−B).
Examples Preform the Following operations if they
are possible. If it is not
possible, please explain why.
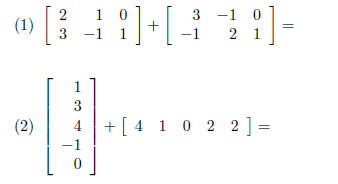
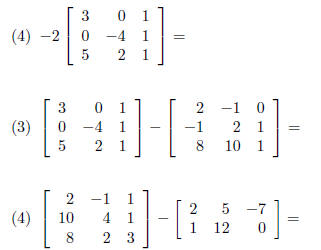
Definition The zero matrix is any matrix with all
its entries equal to 0.
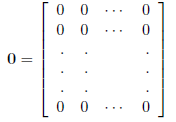
Definition The additive inverse of a matrix A, is
the matrix B, such that
A + B = 0.
NOTE: This implies that the additive inverse of A is −A.
Exercise Find the additive inverses of the following matricies.