Operations and fields

1. Operations and their properties

1.1. Binary operations.

Definition 1. A (binary) operation on the set S is a function ◦ : S × S → S.

The customary notation is to write x ◦ y instead of ◦(x, y).

So the criterion for ◦ to be an operation on S is that for all x, y ∈ S, x ◦ y is an element of S.
Another way to say x ◦ y ∈ S for all x, y ∈ S is that S is closed under ◦. Notice that being an
operation is a property of ◦ with respect to S, while being closed is a property of S with respect to
◦. Which is more convenient to say depends on the context. You can use either, but don’t confuse
them. Again, saying things like ◦ is closed makes no sense.

Example 1. ◦ defined by x◦y = x−y is an operation on R because x−y is a real number whenever
x, y ∈ R.

Example 2. ◦ defined by x ◦ y = x/y is not an operation on R because x/y is not always a real
number if x , y ∈ R. E.g. 1 ◦ 0 = 1/0 does not even exist.

Example 3. ◦ defined by x ◦ y = 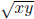is not operation on Q because 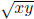is not always a rational
number if x, y ∈ Q. E.g. 1 ◦ 2 = 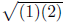is well-known to be irrational.

Exercises: Prove that the following are operations:

1. + on N
2. + on Q
3. + on C
4. · on N
5. · on Q
6. · on C
7. − on Z
8. / on R* = R \ {0} 9. x ◦ y = (x + 1)(y − 1) on C.
10. Composition of functions on the set of functions R → R.
11. Composition of functions on Q[x], which is the set of all polynomials with rational coefficients .

Prove that the following are not operations:

1. − on N
2. / on Q
3. / on Z* = Z \ {0}
4. x ◦ y = 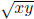on R.
5. Dot product of vectors on R².

1.2. Associativity.

Definition 2. An operation ◦ on the set S is associative if (x◦y)◦z = x◦(y ◦z) for all x, y, z ∈ S.

Notice that commutativity and associativity are properties of the operation ◦ and not of the set
S. Saying things like R is associative makes about as much sense as claiming that the temperature
is purple today.

Example 4. · on Z is associative because (xy)z = x(yz) for any integers x, y.

Example 5. − on Z is not associative because (x−y)−z ≠ y−(x−z) in general, e.g. (0−1)−1 ≠ 0 − (1 − 1).

Example 6. Composition of functions on the set of functions R → R is associative. To see this we
need to convince ourselves that (f ◦ g) ◦ h = f ◦ (g ◦ h) for any functions f, g, h. We are comparing
two functions here. Two functions are equal if they have the same domain and codomain and their
values agree on all elements of this common domain. Both (f ◦ g) ◦ h and f ◦ (g ◦ h) have R for the
domain and the codomain. So let’s see if they agree for all x ∈ R.

(f ◦ g) ◦ h(x) = f ◦ g(h(x)) = f(g(h(x)))
f ◦ (g ◦ h)(x) = f(g ◦ h(x)) = f(g(h(x)))

These are indeed the same for all x.

Exercises: Which of the following operations are associative?

1. · on C
2. / on Q* = Q \ {0} 3. x ◦ y = (x + 1)(y − 1) on C
4.

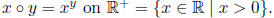
1.3. Commutativity.

Definition 3. An operation ◦ on the set S is commutative if x ◦ y = y ◦ x for all x, y ∈ S.

The “for all” part in this definition is crucial. Given any operation on any set, it’s easy to find
two elements x, y ∈ S such that x ◦ y = y ◦ x. E.g. you could just take y = x. The real question is
whether you can find x, y ∈ S such that x ◦ y ≠ y ◦ x. If not, ◦ is commutative.

Example 7. + on Z is commutative because x + y = y + x for any integers x, y.
Example 8. − on Z is not commutative because x − y ≠ y − x in general, e.g. 0 − 1 ≠ 1 − 0.
Example 9. Composition of functions on the set of functions R → R is not commutative because
f ◦ g ≠ g ◦ f in general. E.g. let f(x) = −x and g(x) = x². Then f ◦ g(x) = f(g(x)) = −x² and
g ◦ f(x) = g(f(x)) = (−x)2 = x² are not the same.

Exercises: Which of the following operations are commutative?

1. · on R
2. · on C
3. / on Q* = Q \ {0}

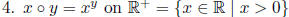
1.4. Identity.

Definition 4. Given an operation ◦ on a set S, we say e ∈ S is an identity if e ◦ x = x for all
x ∈ S and x ◦ e = x for all x ∈ S.

Example 10. For + on Z, 0 is an identity because 0 + x = x = x + 0 for all x ∈ Z.

Example 11. For composition on the set of functions R → R, the identity function f(x) = x is
an identity since f ◦ g(x) = f(g(x)) = g(x) and g ◦ f(x) = g(f(x)) = g(x) for every function g.

Example 12. The operation x ◦ y = xy − 1 on Z has no identity. If y ∈ Z were an identity, it
would have to satisfy x = x ◦ y = xy−1 for all x. In particular, if x = 1, we get y = 2 and if x = 2
we get y = 3/2, and y cannot be both at the same time, not to mention that 3/2 is not even in Z

Example 13. The operation x ◦ y = 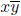on C does not have an identity either. If y ∈C were an
identity, it would have to satisfy x = x ◦ y = 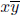for all x ∈ C, which suggests 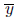= 1 and hence
y = 1. But 1 ◦ x = 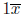≠ x in general. E.g.

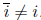
Exercises: Which of the following operations have identities and what are they?

1. − on Z
2. + on the set of all functions R → R (recall f + g is defined by (f + g)(x) = f(x) + g(x))
3. / on R*
4. x ◦ y = (x + 1)(y − 1) on C
5.

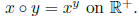
Proposition 1. If an operation ◦ on the set S has an identity, this identity is unique.

Proof: Suppose e and f are both identities. Using the fact that e is an identity, e ◦ f = f. Now
using the fact that f is an identity, e ◦ f = e. So

e = e ◦ f = f.

1.5. Inverses.

Definition 5. Let ◦ be an operation on the set S and assume ◦ has an identity e. We say that
x ∈ S has an inverse if there exists a y ∈ S such that x ◦ y = e and y ◦ x = e.

Example 14. Consider + on Z. We know 0 is the identity (we can say “the” identity because we
now know there can only be one). Every x ∈ Z has an inverse, namely −x because x + (−x) = 0
and (−x) + x = 0.

Example 15. Consider · on R. We know 1 is the identity. The element 2 then has inverse 1/2.
The element 0 has no inverse because no matter what you multiply 0 by , you never get 1. In fact,
if x ∈ R and x ≠ 0, then x has inverse 1/x with respect to this operation.

Example 16. Consider composition on all functions R → R. We know that the identity is f(x) =
x. The function g(x) = x − 1 has inverse g^-1(x) = x + 1. The function g(x) = 3x has inverse
g^-1(x) = x/3. The function g(x) = x² has no inverse because it is not one-to-one. (Why can’t a
function that is not one-to-one have an inverse?) The function f(x) = e^x has no inverse either
because it is not onto. You might now say, but wait, I learned in precalculus that the inverse of e^x
is log(x). But the problem is that log(x) is not a function R → R because its domain only includes
the positive real numbers. So the way we defined our operation, e^x has no inverse. In fact, the
function has an inverse with respect to our operation iff it is both one-to-one and onto.

Exercises: Which of the following operations are such that every element of the underlying set
has an inverse?

1. · on Z⁺ = {x ∈ Z | x > 0}
2. Composition of functions on Q[x], which is the set of all polynomials with rational coefficients.
3. · on the set of all functions R → R (recall fg is defined by (fg)(x) = f(x)g(x))
4. · on R[x], the set of all polynomials with real coefficients
5. · on R(x), which is the set of all rational functions with real coefficients.

Proposition 2. Let ◦ be an associative operation on the set S and assume that it has an identity
e. If x ∈ S has an inverse, then this inverse is unique.

In other words, an element can have no inverse, or one inverse, but it cannot have two distinct
inverses. The proof is similar to the proof that an identity is unique and is left as an exercise. Can
you find an example of an operation with an identity for which inverses don’t have to be unique? By
the above theorem, such an operation would have to be nonassociative. (Finding such an example
may be quite hard.)

2. Fields

Definition 6. A field is a set F with two operations + and · such that

1. + and · are both commutative and associative
2. + has an identity denoted by 0 ∈ F
3. · has an identity denoted by 1 ∈ F
4. Every element has an inverse with respect to +
5. Every element except 0 has an inverse with respect to ·
6. + and · are distributive, which means x · (y + z) = x · y + x · z for all x, y, z ∈ F
7. 0 ≠ 1

Note that + and · may have nothing to do with the addition and multiplication of numbers you
are familiar with. But their properties indeed mimic those of usual addition and multiplication.
The operation + is referred to as addition and · is referred to as multiplication. · is usually omitted
in formulas , just like multiplication of numbers. 0 is called zero and 1 is called one, although they
may have nothing to do with the real numbers 0 and 1. The rules about additive and multiplicative
inverses in essence say that you can subtract any element from any element and you can divide any
element by any nonzero element (0 has no multiplicative inverse).

Example 17. R with ordinary addition and multiplication is a field. In this case the additive
identity and the multiplicative identity are the numbers 0 and 1 you are familiar with. The additive
inverse of a number is its usual negative and the multiplicative inverse is the usual reciprocal.
(Notice 0 has no reciprocal, but it doesn’t have to have a multiplicative inverse.) Commutativity,
associativity, and distributivity are properties you learned about long ago.

Example 18. Z with ordinary addition and multiplication is not a field because not every nonzero
element has a multiplicative inverse. E.g. 2 does not.

Example 19. The subset 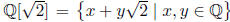x, y ∈ Q of R is a field with usual addition and
multiplication. In fact, we can say it is a subfield of R. It is closed under + because

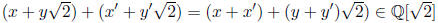
It is closed under · because

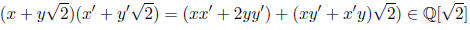
It has additive and multiplicative identities 0 = 0 + 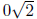and 1 = 1 + 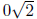. The element x +
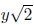
has an additive inverse because

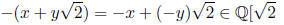
If x + 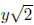≠ 0, that is at least one of x or y is not 0, then it has multiplicative inverse because

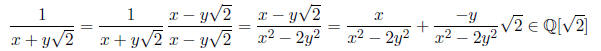
(Why can’t 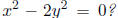Remember x, y are rational numbers.) The two commutativity and
associativity axioms and the distributivity axiom hold because they hold for + and · on R, which
contains .

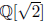Example 20. Consider the set of all functions R → R with addition defined by (f + g)(x) =
f(x) + g(x) and multiplication fg(x) = f(g(x)). In other words, multiplication is composition
here. Is this a field? You can easily check that addition is indeed an operation, is commutative
and associative, has the zero function f(x) = 0 for identity, and every function f has an inverse
−f defined by (−f)(x) = −f(x). The multiplication (which is composition in this case) is an
operation, is associative, and has the identity function f(x) = x for an identity. But it is not
commutative, and not every nonzero function has a multiplicative inverse. For example, f(x) = x²
is not invertible because it is not one-to-one. Distributivity also fails:

[f(g + h)](x) = f(g(x) + h(x))
(fg + fh)(x) = f(g(x)) + f(h(x))

which are in general not equal. E.g. try f(x) = x², g(x) = x, and h(x) = x.

Example 21. The set {1} with addition defined as 1 + 1 = 1, and multiplication 1 · 1 = 1 is not a
field. Actually, it satisfies almost all axioms. It even has an additive identity and a multiplicative
identity. But they are the same thing, so it fails the axiom 0 ≠ 1.

Exercises: Which of the following are fields?
1. C with usual addition and multiplication.
2. Q with usual addition and multiplication.
3. The set of all functions R → R with usual addition and multiplication of functions.
4. The set of all functions f : R → R such that f(x) ≠ 0 for any x ∈ R with usual addition and
multiplication of functions.
5. R(x), the set of all (formal) rational functions with real coefficients with usual addition and
multiplication of functions. That they are formal rational functions means you don’t have
to worry about what the domain is when you add and multiply them.
6. The subset Z[i] = {x + yi | x, y ∈ Z} of C with ordinary addition and multiplication.
7. The subset Q[i] = {x + yi | x, y ∈ Q} of C with ordinary addition and multiplication.