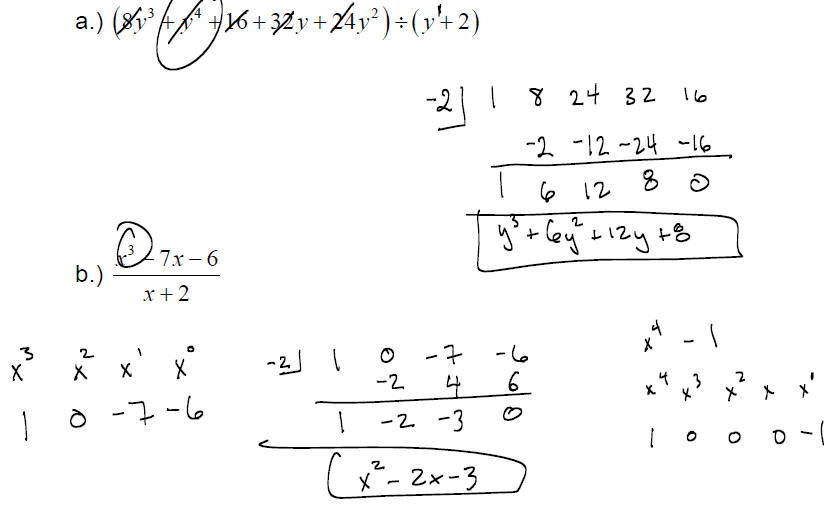Dividing Polynomials by Polynomials; Synthetic Division

6.6 Dividing Polynomials by Polynomials ; Synthetic Division
Division of a polynomial by a polynomial like (x² + 2x −15)÷ (x + 5) is very similar to
the long division process we use to divide whole numbers . Let’s review this

procedure first:

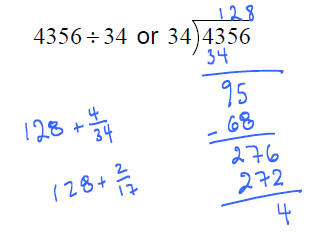
• 4356 is called the
dividend
• 34 is called the divisor
• the answer is called the
quotient

Divide, Multiply, Subtract, pull
down.

We write the answer as:

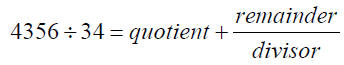
We check the answer by: quotient * divisor + remainder = dividend

What happens if we get a zero remainder when dividing?
______________________

We follow a similar procedure for division of a polynomial by a binomial .

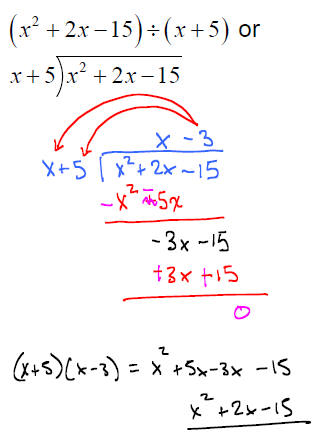
x² + 2x −15 is called the dividend x + 5 is
called the divisor the answer is called the
quotient

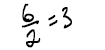
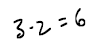
PROCEDURE:
1.) Divide the first term in the dividend by
the first term in the divisor. This is the first
term in the quotient.
2.) Multiply this by each term in the
divisor.
3.) Subtract.
4.) Bring down
Repeat the process until the remainder
can no longer be divided.

We write the answer as:

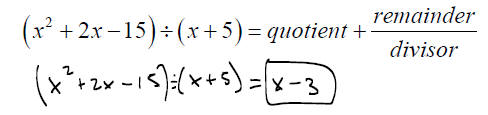
We check the answer by making sure that:
quotient * divisor + remainder = dividend

GENERAL PROCEDURE:

1. Write the polynomials in standard form. (in order with descending
powers ) If there is a missing term, fill it in with a zero times the missing
variable part . (i.e. x² +1 = x² + 0x +1)

2. Divide the first term in the dividend by the first term in the divisor. This is
the first term in the quotient.

3. Multiply each term in the divisor by the result of the previous step . Write
the answer beneath the dividend with similar terms under each other.

4. Subtract the product from the dividend .

5. Bring down the next terms and treat this as the new dividend. Start the
process over again. Repeat this until the remainder can no longer be
divided. This happens when the degree of the remainder is less than
the degree of the divisor.

EXAMPLE: Divide

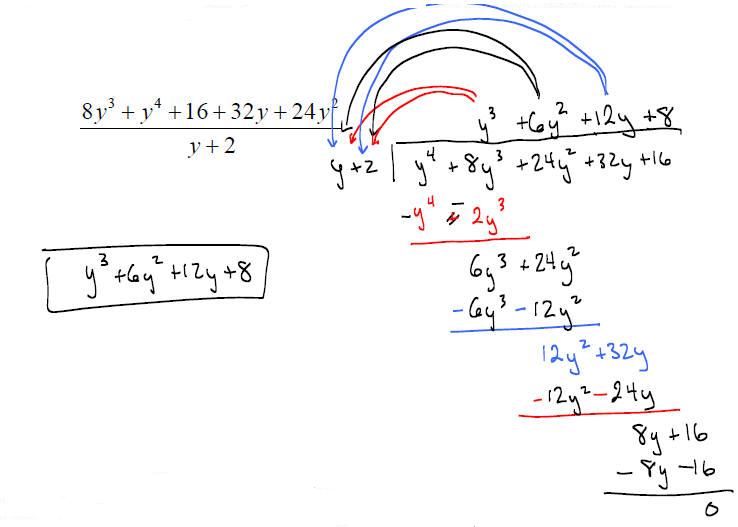
EXAMPLE: Divide:

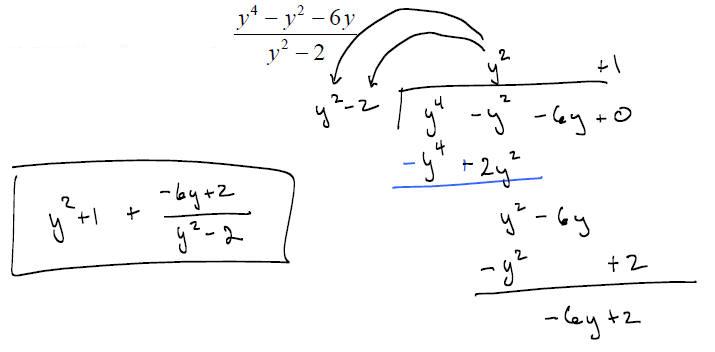
EXAMPLE: Divide:

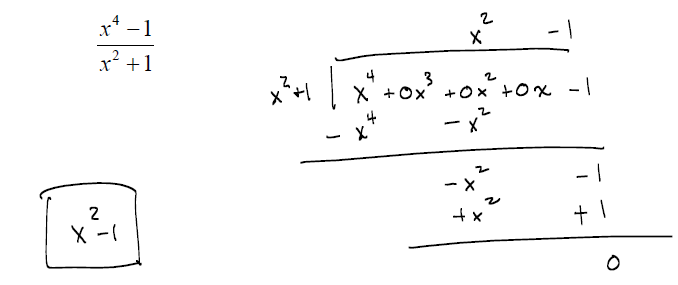
EXAMPLE: Divide:

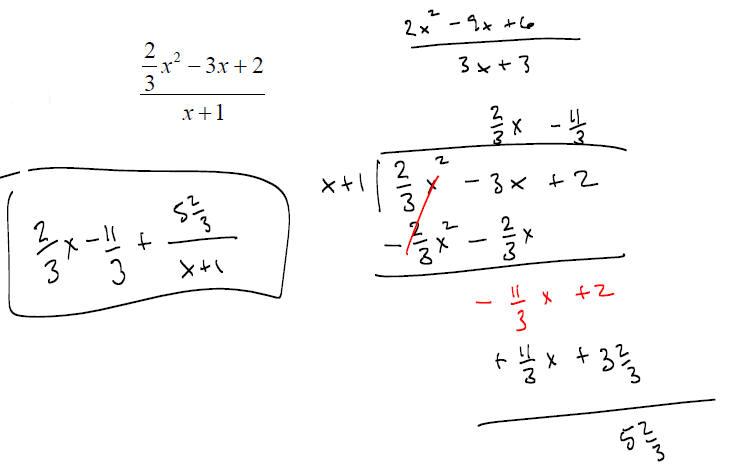
SYNTHETIC DIVISION :
We can use synthetic division to divide polynomials if the divisor is of the form
x − c. This method is quicker than long division.
Let’s see how the method works with
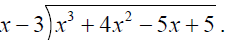
LONG DIVISION:

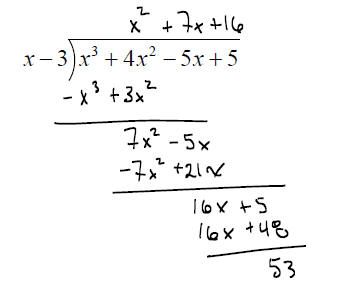
SYNTHETIC DIVISION:

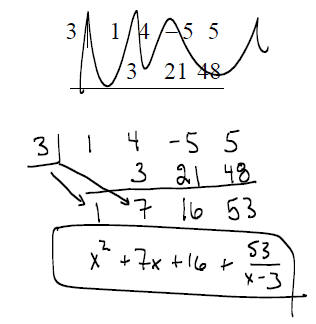
EXAMPLE: Use synthetic division to divide