The California Mathematics Content Standards
Trigonometry uses the techniques that students have
previously learned from the study
of algebra and geometry . The trigonometric functions studied are defined
geometrically
rather than in terms of algebraic equations. Facility with these functions as
well as the
ability to prove basic identities regarding them is especially important for
students
intending to study calculus, more advanced mathematics, physics and other
sciences,
and engineering in college.
| |
1.0 Students understand the notion of angle and how
to measure it, in both degrees
and radians. They can convert between degrees and radians. |
Note: The sample
problems illustrate
the standards and
are written to help
clarify them. Some
problems are written
in a form that can be
used directly with
students; others will
need to be modified
before they are
used with students. |
| |
2.0 Students know the definition of sine and cosine as y- and
x- coordinates of
points on the unit circle and are familiar with the graphs of the sine
and cosine
functions.
Find an angle β between 0 and 2π such that cos (β) =
cos (6π/7)
and sin (β) = -sin (6π/7). Find an angle θ between 0 and
2π such
that sin (θ) = cos (6π/7) and cos (θ) = sin (6π/7).
|
|
| |
3.0 Students know the identity cos2(x) + sin2 (x)
= 1:
3.1 Students prove that this identity is equivalent to the Pythagorean
theorem (i.e., students can prove this identity by using the Pythagorean
theorem and, conversely, they can prove the Pythagorean theorem as a
consequence of this identity).
3.2 Students prove other trigonometric identities and simplify others by
using the identity cos2 (x) + sin2 (x) = 1. For
example, students use this
identity to prove that sec2 (x) = tan2 (x) + 1.
|
|
| |
4.0 Students graph functions of the form f(t) = A sin (Bt + C) or f(t) =
A cos
(Bt + C) and interpret A, B, and C in terms of amplitude, frequency,
period,
and phase shift.
On a graphing calculator, graph the function f(x) = sin (x) cos (x).
Select a
window so that you can carefully examine the graph.
1. What is the apparent period of this function?
2. What is the apparent amplitude of this function?
3. Use this information to express f as a simpler trigonometric
function.
|
|
| |
5.0 Students know the definitions of the tangent and cotangent functions
and can
graph them.
|
|
| |
6.0 Students know the definitions of the secant and cosecant functions
and can
graph them.
|
|
| |
7.0 Students know that the tangent of the angle that a line makes with
the x-axis is
equal to the slope of the line.
|
|
| |
8.0 Students know the definitions of the inverse trigonometric functions
and can
graph the functions.
|
|
| |
9.0 Students compute, by hand, the values of the trigonometric functions
and the
inverse trigonometric functions at various standard points.
|
|
| |
10.0 Students demonstrate an understanding of the addition formulas for
sines and
cosines and their proofs and can use those formulas to prove and/or
simplify
other trigonometric identities.
Use the addition formula for sine to find an expression for sin (75°).
|
|
| |
11.0 Students demonstrate an understanding of half-angle and
double-angle formulas
for sines and cosines and can use those formulas to prove and/or
simplify
other trigonometric identities.
|
|
| |
12.0 Students use trigonometry to determine unknown sides or angles in
right
triangles.
|
|
| |
13.0 Students know the law of sines and the law of cosines and apply
those laws to
solve problems.
A vertical pole sits between two points that are 60 feet apart. Guy
wires to the
top of that pole are staked at the two points. The guy wires are 40 feet
and 35
feet long. How tall is the pole?
|
|
| |
14.0 Students determine the area of a triangle, given one angle and the
two adjacent
sides.
|
|
| |
15.0 Students are familiar with polar coordinates. In particular, they
can determine
polar coordinates of a point given in rectangular coordinates and vice
versa.
|
|
| |
16.0 Students represent equations given in rectangular coordinates in
terms of polar
coordinates.
Express the circle of radius 2 centered at (2, 0) in polar coordinates.
|
|
| |
17.0 Students are familiar with complex numbers. They can represent a
complex
number in polar form and know how to multiply complex numbers in their
polar form.
|
|
| |
18.0 Students know DeMoivre’s theorem and can give nth roots of a
complex
number given in polar form.
|
|
| |
19.0 Students are adept at using trigonometry in a variety of
applications and word
problems.
A lighthouse stands 100 feet above the surface of the ocean. From what
distance
can it be seen? (Assume that the radius of the earth is 3,960 miles.)
|
|
This discipline combines many of the trigonometric,
geometric, and algebraic techniques
needed to prepare students for the study of calculus and strengthens their
conceptual
understanding of problems and mathematical reasoning in solving problems. These
standards take a functional point of view toward those topics. The most
significant new
concept is that of limits. Mathematical analysis is often combined with a course
in trigonometry
or perhaps with one in linear algebra to make a yearlong precalculus course.
Note: The sample
problems illustrate
the standards and
are written to help
clarify them. Some
problems are written
in a form that can be
used directly with
students; others will
need to be modified
before they are
used with students. |
1.0 Students are familiar with, and can apply, polar
coordinates and vectors in the
plane. In particular, they can translate between polar and rectangular
coordinates
and can interpret polar coordinates and vectors graphically. |
|
| |
2.0 Students are adept at the arithmetic of complex numbers. They can
use the
trigonometric form of complex numbers and understand that a function of
a
complex variable can be viewed as a function of two real variables. They
know
the proof of DeMoivre’s theorem.
|
|
| |
3.0 Students can give proofs of various formulas by using the technique
of
mathematical induction.
Use mathematical induction to show that the sum of the interior
angles in a
convex polygon with n sides is ( n - 2)×180°.
|
|
| |
4.0 Students know the statement of, and can apply, the fundamental
theorem
of algebra.
Find all cubic functions of x that have zeros at x = -1 and x = 2 and
nowhere
else. (ICAS 1997)
|
|
| |
5.0 Students are familiar with conic sections, both analytically and
geometrically:
5.1 Students can take a quadratic equation in two variables; put it in
standard form by completing the square and using rotations and
translations, if necessary; determine what type of conic section the
equation represents; and determine its geometric components (foci,
asymptotes, and so forth).5.2 Students can
take a geometric description of a conic section—for
example, the locus of points whose sum of its distances from (1, 0)
and (-1, 0) is 6—and derive a quadratic equation representing it.
|
|
| |
6.0 Students find the roots and poles of a rational function and can
graph the
function and locate its asymptotes.
|
|
| |
7.0 Students demonstrate an understanding of functions and equations
defined
parametrically and can graph them.
Sketch a graph of f(x) = (x - 2)2 -1. Sketch the graphs of
g(x) = f(|x|)
and of h(x) = |f(x)|. Looking at your graph of h(x), identify a value of
x
for which h(x + 1) = h(x) -3.
|
|
| |
8.0 Students are familiar with the notion of the limit of a sequence and
the limit of
a function as the independent variable approaches a number or infinity.
They
determine whether certain sequences converge or diverge.
|
|
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
February 5th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
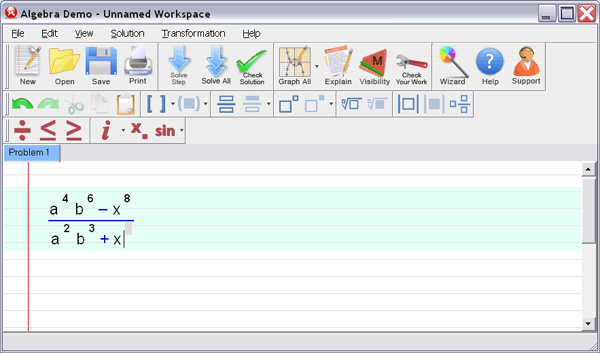
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
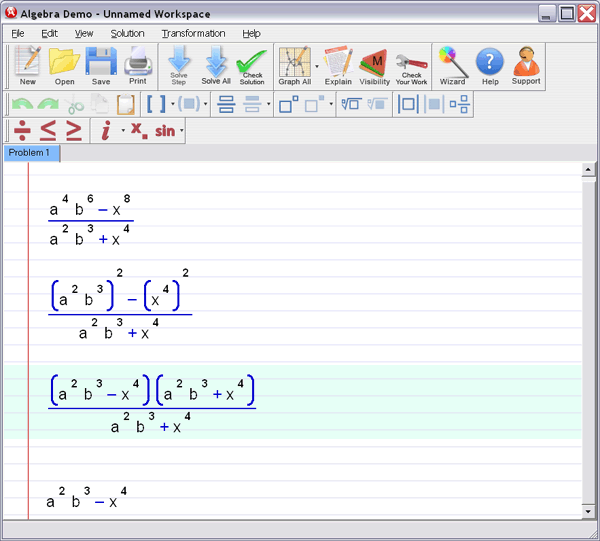
Step 2 :
Let Algebra Helper solve it:
Step 3 : Ask for an explanation for the steps you don't understand:
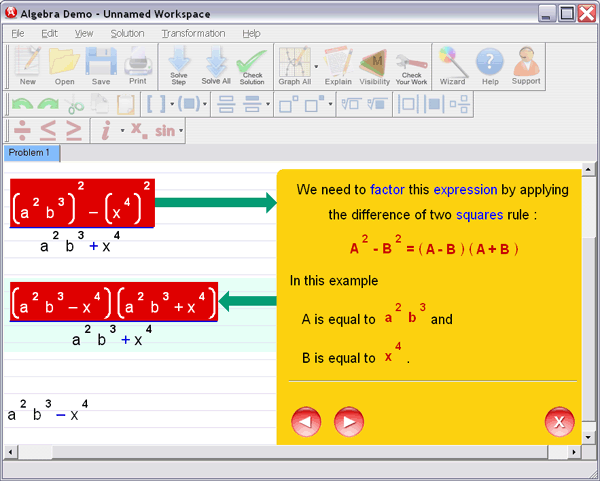
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



