Intermediate Algebra Summary

This is an overview of the key ideas we have discussed during the first part of this course.
You may find this summary useful as a study aid, but remember that the only way to really
master the skills and understand the ideas is to practice solving problems .

---

The Addition Method (For Solving Systems of Linear Equations)
Write both equations in the form ax + by = c; multiply each equation by a constant, if
necessary, so that the coefficients of one of the varibales are the same size; then either add or
subtract the two equations in order to eliminate one of the variables; solve for the remaining
variable ; then plug that value back into one of the original equations to solve for the other
unknown .

Example: Solve the system of linear equations:
2x + 5y = 8
3x + 4y = 1

Solution: Begin by multiply the first equation by 3 and the second equation by 2, so that
the coefficients of x match up:
6x + 15y = 24
6x + 8y = 2

Then subtract the second eqution from the first to eliminate x :
7y = 22.

Hence
y =22/7.

Now we plug this into the original first equation to get

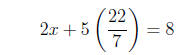
Therefore

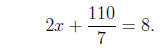
Then we isolate x: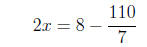

so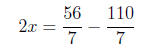

therefore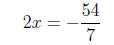

and consequently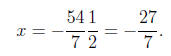

So the answers are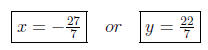

---

Solving Absolute Value Equations
Example: Solve the equation |3x + 4| = 2.
Solution: Either
3x + 4 = 2 or 3x + 4 = −2

Hence
3x = −2 or 3x = −6

Therefore

---

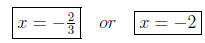
The Point- Slope Formula for a Line
Example: Find the equation for a line through the points (2, 5) and (−3, 2).
Solution: First we find the slope:

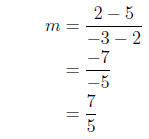
Now we plug this slope and either point into the formula y = y₁ = m(x − x₁) to get

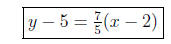
That is the equation for the line. If we need to, we can simplify and solve for y:

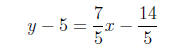
so

---

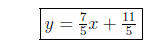
Solving Quadratic Equations by Factoring
Example: Solve the equation x² = 5x + 24 by factoring.
Solution: First, we need to move all the terms to one side of the equation, so we subtract
5x from both sides, and we subtract 24 from both sides to get
x² − 5x − 24 = 0

Now we factor the left side:
(x − 8)(x + 3) = 0

The only way this can be true is if one of the two factors is zero, so we see taht either
x − 8 = 0 or x + 3 = 0

Consequently,

---

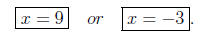
Solving Quadratic Equations by Completing the Square
Example: Solve the equation 3x² = 10x + 6 by completing the square.
Solution: We need to get all the terms with x or x² on the same side, so we subtract 10x
from both sides:
3x² − 10x = 6

We also need the coefficient of x to be 1, so we divide both sides of the equation by 3:

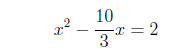
Now we complete the square: the coefficient of x on the left side i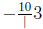s ; half of this is −5/3 ;the square of −5/3 is 25/9 , so that’s what we need to add to both sides:

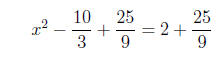
Since 2 = 18/9 , we can write this as

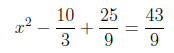
Now we factor the left side:

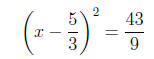
Then take square roots of both sides:

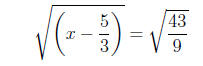
Therefore

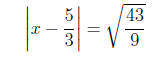
Hence either

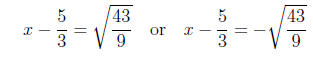
so

---

Function Notation
Example: Suppose that a function is given by the formula f(x) = x² − 2x. Find f(2) and
f(−3).
Solution: We evaluate the function by plugging the appropriate value in for x and simpli-
fying:

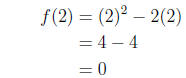
Similarly,

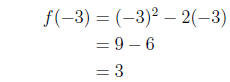
So we have

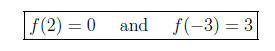
Example: Find a formula for a linear function f(x) that satisfies f(2) = 7 and f(4) = −1.
Solution: First we find an equation for a line that passes through the points (2, 7) and
(4,−1) – we can so this using the point-slope formula:

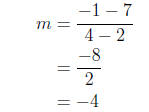
Therefore
y − (−1) = −4(x − 4)

so
y + 1 = −4x + 16

Therefore
y = −4x + 15

Now we replace the y with f(x) to obtain function notation:

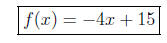
TI-84 Calculator Reference Guide - Entering and Using Data Tables

ENTERING LISTS
Most statistical calculations involve working with tables of data, so we need
to be able to input such tables into the graphing calculator . In the following
example, we will enter the data in the table at right. The same data will be
used in the later examples in this guide.

x	2	3	7.2	8.1	108
y	5	8	9	9

1. Select the STAT menu by
pressing:

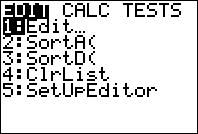
2. Select the first item in order to
edit the calculator’s lists:

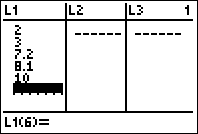
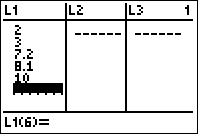
3. Enter the x-values in the first
column, labeled L1, as follows:

4. Use the right arrow key to move
the cursor to the first row of the
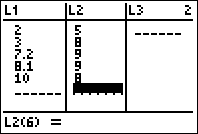
second column (labeled L2); then
enter the y-values as follows:

SCATTERPLOTS
You can plot individual points on an xy-plane by performing a scatterplot.
1. First, set the window as you
would when graphing a function.
To got to the menu for this,
press:

2. Go to the STAT PLOT menu by
pressing:

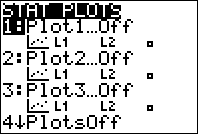
3. Select the first plot by pressing 1
or enter :

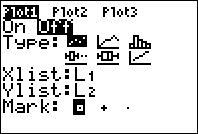
4. Select On by pressing enter:

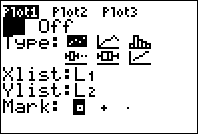
5. View your plot by pressing:

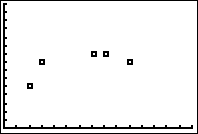
REGRESSIONS
You can fit a line or curve to a set of data points by performing a regression with the
graphing calculator. In this example, we find a line of best fit using a linear regression.
1. Go to the STAT menu by
pressing:

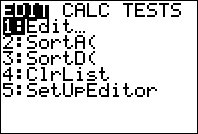
2. Use the right arrow key to select
the CALC menu:

3. Select LinReg(ax+b) to perform a
linear regression on the data in
lists L1 (for x-values) and L2(for
y-values):

4. Calculate the coefficient for the
regression by pressing:

5. The resulting screen gives you
the coefficients for the
regression, as well as the
correlation coefficient r and its
square.