1. Make time in your schedule to learn; you
cannot take shortcuts.
2. Read each section in your textbook and answer the questions in the
study
guide before you go to class.
To read a section, first read the objectives, headings, and any boxed
information. This will give you a preview of what to expect. Then, read
the
section carefully, trying the examples and filling in missing steps. If
you
don’t understand something, write your question in the margin next to
the
words or problem you don’t understand.
3. Take notes in class, trying to understand as the teacher presents
examples and explains concepts.
4. Do your homework (It should be easier after the previous two steps ).
Make sure to understand what you are doing and be able to solve each
problem completely and correctly by yourself.
5. Carry on a conversation with yourself as you work, asking as you
start
each problem, “What is this? What is my goal? What should my answer look
like when I am done?” Then, as you work a problem ask, “ What property
allows me to take this step?” And at the end, “ Does my answer make
sense?
How can I check it?”
6. Maintain a great attitude about learning Algebra; people who have a
good
attitude find it easier to learn, and those who learn algebra well
usually
enjoy it.
7. Go to the lab or your instructor’s office and get help when you need
it. |
Section 6.1 Factoring Polynomials with Common Factors
Read section 6.1, pages 322 – 326 and answer the following questions as you
read:
1. What is factoring?
2. Circle all the polynomials below that are factored. How do you know
they are factored?
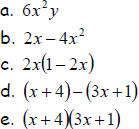
*Which of the expressions above are equivalent?
3. Explain how to find the greatest common factor of two monomials. If
it helps, use #4 as an example.
4. Find the greatest common factor of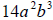 
and
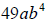
5. Factor out the greatest common factor from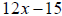 
.
How do you
know what to put in the parentheses?
6. Factor the greatest common monomial factor from
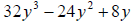
Check your answer using the distributive property .
7. Factor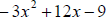 
in two ways:
a. Factor out a common monomial factor of 3
b. Factor out a common monomial factor of –3
8. Give an example of a binomial whose greatest common factor is 5x.
Then, factor it.
9. Underline the common binomial factors in the following polynomials,
and then factor the binomials out. Some polynomials may not have a
common binomial factor, in which case you will not be able to factor it.
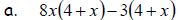
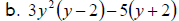
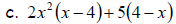
10. Factor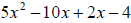 
by grouping
11. The area of a rectangle can be represented by the polynomial .
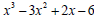Find the dimensions of the rectangle.
(Explain how you
know these must be the dimensions.)
12. Find a polynomial that factors as
.
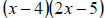Section 6.2 Factoring Trinomials
Read section 6.2, pages 330 – 334 and answer the following questions as you
read:
1. Warm up: find all pairs of numbers that multiply to 36.
2. FOIL each of the following expressions but do not combine like terms .
You are going to factor the results, so leave space.
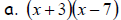
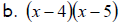
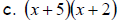
3. Factor each of your answers in #1 by grouping. What do
you notice
about the factored form and the original expression?
4. To factor the trinomial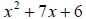 
we must find two
numbers whose
__________ is 7 and whose __________ is 6. What are the two
numbers? Factor the trinomial. FOIL to check your answer.
5. To factor the polynomial
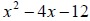we must find two numbers whose
product is _____ and whose sum is ______. Factor the trinomial. FOIL to
check your answer.
6. In the ‘Guidelines for Factoring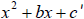 
why must
m and n have
unlike signs if c is negative ?
7. Factor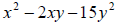 
8. How do you know when you have factored completely?
9. Factor completely: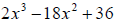
10. What do we call a trinomial that cannot be factored?
Section 6.3 Relations, Functions, and Graphs
Read section 6.3, pages 338 – 342 and answer the following questions as you
read:
1. Read the objectives. What is different from what you
have already
learned?
*Skip the first five examples since we will not use this method to factor . Go
right to the middle of page 341 and start at ‘Factoring by Grouping’.
2. Rewrite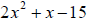 
with four terms so that it
can be factored by
grouping.
3. To factor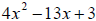 
we must find two numbers that
multiply to
______ and that add to ______.
Use a table to find the two numbers.
Rewrite the trinomial with four terms so it can be factored.
Factor.
4. Factor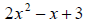 
showing all the steps as in .
5. How can you check your answer after you have factored?
6. List all the types of factoring you have learned so far
in this chapter.
Give an example for each type.
