Quadratic Functions

A quadratic function is a function Q(x) of the form

For example, Q(x) = 3x² − 7x + 5 is a quadratic function, and here a = 3, b = −7 and c = 5.
Although ax²+bx+c is probably the form we are most familiar with from high school for quadratic
functions, this is not what we refer to as standard form. Standard form for a quadratic function
means write the quadratic function in the form:

Standard From: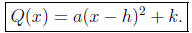

Tip! The “a” value in standard form is the same “a” in the form ax² + bx + c.

Why standard form is useful. Standard form is the most useful form for a quadratic function
because it tells you the most important information about the function. Namely, (h, k) is the
vertex of the graph of Q(x). If a > 0 the graph opens up; if a < 0 the graph opens down:

Graph of y = a(x − h)2 + k with a > 0	Graph of y = a(x − h)2 + k with a < 0

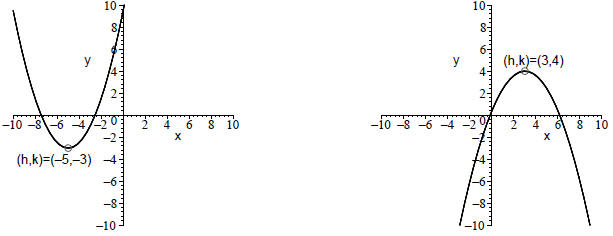This hand-out will explain several methods for putting a quadratic function in standard form. You
do not need to learn all the methods. But, everyone should learn at least one algebraic method.
Different people find different methods easier to use.

Algebraic method #1 (completing the square). This method is perhaps the fastest when the
numbers are nice. People who do not memorize formulas well, but who are good at doing algebra
in their head tend to like this method . If you are not good at algebra in your head, you should
probably concentrate on the other methods. Let us put the quadratic function Q(x) = 3x²+36x+1
in standard form.

Step 0: Write the function in decreasing powers of x: Q(x) = 3x² + 36x + 1

Step 1: Factor out the “a” from the first two terms: Q(x) = 3(x² + 12x) + 1.

The tricky step is to try to make x² + 12x look like a perfect square. That is, we want to find
something so



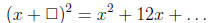
Note that



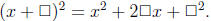
Thus, we divide 12 by 2 to get 6 and consider (x + 6)² = x² + 12x + 36. Notice this matches
x² + 12x except for the constant term.

Step 3: perfect square: Q(x) = 3(x² + 12x + 36 − 36) + 1.

Notice we have added and subtracted 36 so we haven’t changed anything.

Step 4: Factor the perfect square: Q(x) = 3((x + 6)² − 36) + 1.

Step 5: Combine the constant terms: Q(x) = 3(x+6)²−3·36+1 = 3(x+6)²−107.

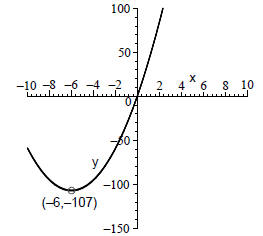
Thus Q(x) = 3(x + 6)² − 107 is standard form, and we see immediately that the vertex is
(−6,−107). Because a = 3 > 0, we know the parabola opens up, and so the minimum value
of Q is −107 and it occurs when x = −6.

Algebraic method #2 (work backwards). This method is good for people who do not memorize
well and find the previous method difficult to do. The idea here is to multiply out standard form.
Let’s take the same example.

Step 0: Write the function in decreasing powers of x: Q(x) = 3x² + 36x + 1

Step 1: Set equal to standard form: 3x² + 36x + 1 = 3(x − h)² + k.

Note that we have made use of the fact that the a values are the same in the form we started with
and in standard form. That is, we plugged in a = 3 on the right hand side.

Step 2: Multiply out the right-hand side: 3x² + 36x + 1 = 3(x² − 2hx + h²) + k.

Step 3: Continue to multiply out on the right: 3x² +36x+1 = 3x² −6hx+3h² +k.

Step 4: Cancel the x² terms: 36x + 1 = −6hx + 3h² + k.

Now we compare what is in front of “x” on the left and right. On the left we have 36 and on the
right we have −6h. Thus, we must have that 36 = −6h, which we can use to solve for h .

Step 5: solve for h: h = −6.

Now we compare the constant terms on the right and left. We have 1 on the left and 3h2 +k on the
right. Hence 1 = 3h² + k.

Step 6: plug in for h: 1 = 3(−6)² + k.

Step 7: solve for k: k = 1 − 3(−6)² = −107.

Step 8: plug h and k into standard form: Q(x) = 3(x−(−6))²−107 = 3(x+6)²−107.

Algebraic method #3 (memorize a formula). This is the method for you if you are good at
memorizing formulas. If you can memorize the formula, and especially if the numbers are bad and
you have a calculator to help you multiply, then this is certainly the easiest way that will always
work.
Step −1: memorize the formula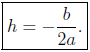

Step 0: Write the function in decreasing powers of x: Q(x) = 3x² + 36x + 1

Step 1: Use the formula: .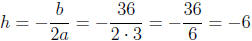

Step 2: Use k = Q(h): k = Q(−6) = 3(−6)² + 36(−6) + 1 = −107.

Step 3: plug h and k into standard form: Q(x) = 3(x−(−6))²−107 = 3(x+6)²−107.

Algebraic method #4 (factored short-cut). Warning! This method does not work for all quadratic
functions. It is a short-cut that lets you avoid multiplying out if for some reason your quadratic
function is factored. It is worth learning this short-cut because in many word problems, the
quadratic function naturally comes factored. For example, suppose that a rectangle has perimeter
100. Let x be the length of the rectangle. Find the area A as a function of x. Well, we have
that

A(x) = length · width = x(50 − x).

Note that that the 50−x comes from the fact that the perimeter is 100, so length+width = 50. This
function naturally comes factored. To use any of the methods above, we would need to first multiply
this function out. This is not so hard, but it is an extra step. What we can do instead is use a special
fact about quadratic functions: if a quadratic function has zeros, then the vertex is exactly halfway
between the zeros. In this case, we see that A(0) = 0 and A(50) = 0. Half-way between 0 and
50 is 25, so h = 25. To figure out k, we use k = A(h) = A(25) = 25(50 − 25) = 25 · 25 = 625.
Now a is −1, so A(x) = −(x − 25)² + 625 is standard form.

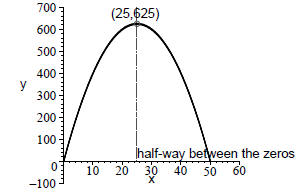
Notice that standard form tells us a lot. It tells us that the most area we can have with a rectangle
with a perimeter of 100 is 625, and it tells us that to get that much area, we need to make its length
be 25.

Graphing Calculator Method. You can also convert to standard form with the help of a calculator.
Plug the formula in using . Graph in a window where you can see the vertex. On the calc menu,
if the parabola opens up, choose “minimum” and if the parabola opens down, choose “maximum.”
This will find the values of h and k for you. Then simply plug into the equation

Q(x) = a(x − h)² + k.

Remember the minus sign before h.

For example, if we look at −2x² + 20x − 43 on a graphing calculator and find the maximum
( because a is negative ), we see

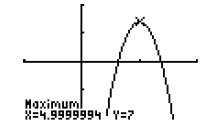
that the vertex is at (5, 7) and so standard form of the equation is: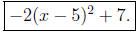

Finding roots (or zeros) of a quadratic function

Algebraic Method #1 (factoring): Suppose we want to solve x² − x − 6 = 0. One approach is to
factor the quadratic function as (x − 3)(x + 2) = 0. Then we observe that we can only multiply
two numbers together and get zero if at least one is zero. So we know x − 3 = 0 or x + 2 = 0.
Solving each of these equations, we find x = 3 and x = −2 as our roots or zeros . Of course this
method is the best method to use if the numbers are easy or the function is already factored.

Algebraic Method #2 (standard form): Finding roots is easy if you put the quadratic function in
standard form, or if it is already in standard form. For example, suppose we want to solve

2(x − 5)² − 50 = 0.

Simply move the 50 to the other side

2(x − 5)² = 50.

Now, divide both side by two:

(x − 5)² = 25.

Thus,

x − 5 = ±5 and hence x = 5 ± 5 = 0, 10.

Thus x = 0 and x = 10 are the two roots.

Algebraic Method #3 (quadratic equation): Everyone should try to memorize this formula. The
roots of the quadratic equation ax² + bx + c = 0 are

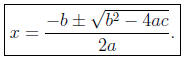
For example, if we want to find the roots of x² − x − 6, then we do

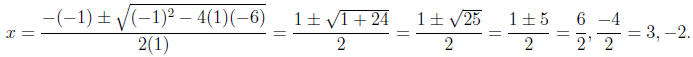
Tip! If you have to solve many equations using the same quadratic function, for example you want
to find out when Q(x) = 0, Q(x) = 1, Q(x) = 2, etc. you should use method 2. Once you put
Q(x) in standard form, it is easy to solve for each of the different values.

Of course you can also use your graphing calculator to find zeros