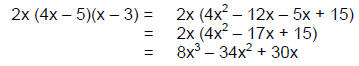Step 1: Look for a GCF and factor it out first.
Step 2: Multiply the coefficient of the leading
term a by the constant term c. List the factors of this product
(a • c) to find the pair of factors, f1 and f2, that sums to
b, the coefficient of the middle term.
• When c is positive , factors of a • c
have the same sign –
o If the middle term bx is positive, both factors
are positive.
o If the middle term bx is negative, both factors are negative.
o Find the pair of factors that adds to b.
• When c is negative , factors of a • c
have opposite signs –
o The larger of these factors has the same sign as the
middle term.
o Find the pair of factors that subtracts to b.
Step 3: Rewrite (split) the middle term bx
using the factors, f1 and f2, found in Step 2. The expression now
has 4 terms:
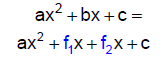
Step 4: Group the terms of the expression into
binomial pairs as shown:
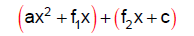
Step 5: Factor out a “gcf” from each pair. If the
expression can be factored by grouping, the terms will share a common "binomial"
factor.
Step 6: Factor out the common binomial factor to
write the factorization.
Step 7: Check the result by multiplying.
EXAMPLE: Factor: 8x^3 – 34x^2 + 30x
Step 1: Factor out the GCF 2x:
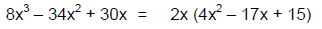
Step 2: Multiply a • c. Here, a = 4,
c = 15, and a • c = 60. Next, list the factors of 60 to
find the pair that adds to the middle term –17x. Note that the factors of
60 are both negative.

Factors of 60 that add to –17 are −5 and −12.
Step 3: Rewrite the middle term –17x using
the factors found in Step 2, −5 and −12:
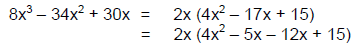
Step 4: Group the terms into binomial pairs as
shown:
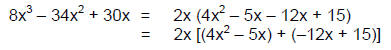
Step 5: Factor out a “gcf” from each group of
terms. The gcf of the first group, (4x2^ – 5x), is x; the gcf of the
second group, (–12x + 15), is −3:

The terms now share a common binomial factor : (4x – 5).
Step 6: Factor out the common binomial factor
(4x – 5) to write the factorization:
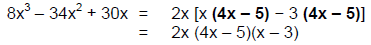
Step 7: Check the result by multiplying: