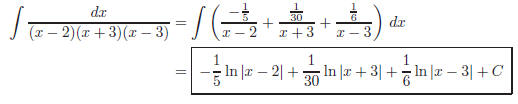2. To determine the constants A and B in the problem, we
first simplify the equation by multiplying by
Q (x):
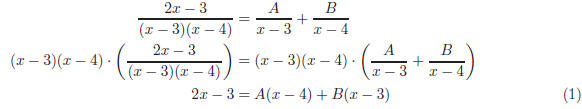
Now plug in 2 different values of x into Equation (1) and
solve for A and B:
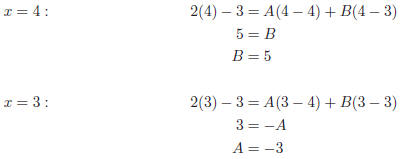
5. Using long division on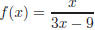 
we
have:
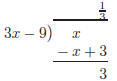
Therefore, f (x) is:
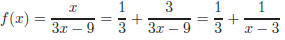
The integral of f (x) is:
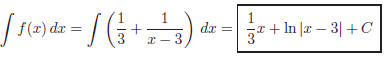
6. Using long division on
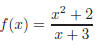we have:
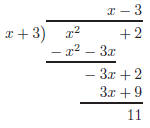
Therefore, f (x) is:
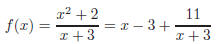
The integral of f (x) is:
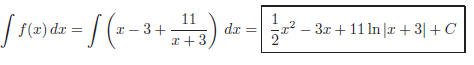
11. To solve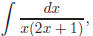 
we use the
method of partial fractions:
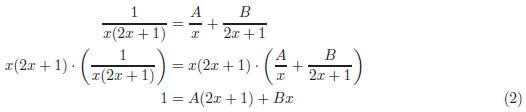
Now plug in 2 different values of x into Equation (2) and
solve for A and B :
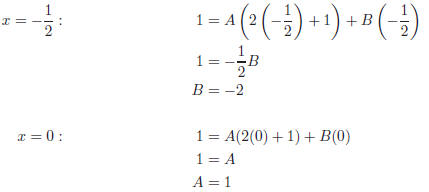
Therefore, the integral is:
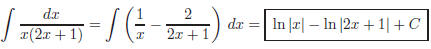
13. To solve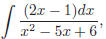 
we use the
method of partial fractions. First, the denominator factors as
follows :
x2− 5x + 6 = (x − 2)(x − 3)
Now separate the quotient into fractions as follows
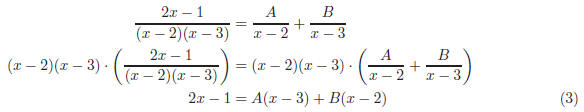
Now plug in 2 different values of x into Equation (3) and
solve for A and B:
Therefore, the integral is:
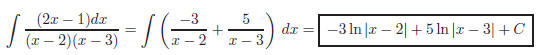
14. To solve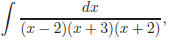
we use the
method of partial fractions :
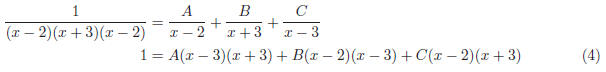
Now plug in 3 different values of x into Equation (4) and
solve for A, B, and C:
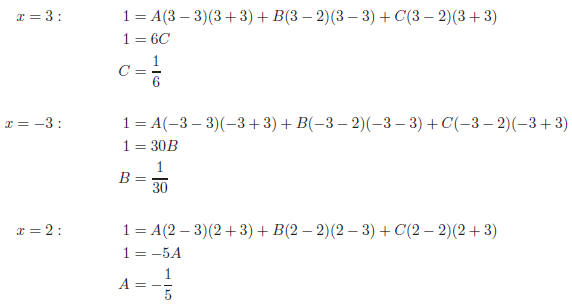
Therefore, the integral is:
