Topics from Chapter 1: Simplify algebraic
expressions
1. Number Line: Be able to plot points on a number (including fractions,
decimals, square roots and other irrational #''s)
2. Ordering symbols: < (remember that "less than" means "to the left of" on the
number line: -10<-5 since -10
is to the left of -5),> greater than, ≤ , ≥ (remember that a line
underneath means "or equal to": 10 ≤ 10 is a true statement
since 10 is less than OR EQUAL TO 10)
3. Absolute Value: Remember that l#l measures the distance from that # to 0 and
distance is always positive !
4. Prime factors: prime numbers are evenly divisible by themselves and 1 only. 9
is not prime since 3 goes evenly into 9
5. Order of operations: PEMDAS
6. Variable expressions: Identify constants, variables, coefficients, terms
7. Evaluate by substituting given values for the variables (use parantheses to
replace the variable to avoid making sign
errors.)
8. Distributive property 2(3x - 5)= 6x -10
9. Removing parantheses : Use distributive property. Remember that -(4x-3)= -4x+
3
10. Combine like terms : When variables and their exponents match, add the
coefficients of the terms.
Topics from Chapter 2:
1. Solve Equations:
Distribute to remove parantheses
Clear fractions by multiplying BOTH SIDES OF EQUATION by the LCD
Move variable terms to left side, non variable terms to the other
Divide by coefficient of variable.
2. Solve word problems: Remember to DEFINE THE VARIABLE, and ANSWER IN WORDS
WITH UNITS!!
3. Solve Inequalities: Graphing on a number line...use open circle for < or >
use closed circle for ≤ or ≥
Remember that multiplying or dividing by a negative switches the direction of
the inequality
Example: -2x> 6, solve by dividing both sides by –2, and you get x <-3
Topics from Chapters 3
1. Plot points: plot any given point, identify the quadrant in which it
lies, know the form of x-intercepts (a, 0)
and y-intercepts (0, b)
Quadrants:
|
Quad II |
Quad I |
|
Quad III |
Quad IV |
2. Find distance (from Section 11.1): Find the
distance between two points by using the Distance Formula
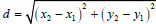 (also be able to plot the points and show
the line segment that represents the distance
(also be able to plot the points and show
the line segment that represents the distance
between the points)
4. Graph line equations by
a. plotting points (create a table of values, i.e. t-chart)
b. finding x-intercept and y-intercept: set x = 0 and find y; set y = 0 and find
x.
c. plotting the y-intercept (or any other point) and using the slope
as rise over run to find another point on the line
5. Find the Slope of a line: Remember that
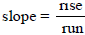 (you have to rise before you can run...think
about it!)
(you have to rise before you can run...think
about it!)
a. given two points :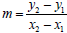
b. given an equation: solve the equation for y to get the point
slope equation y = mx + b.
c. parallel lines: same slope
perpendicular lines: slopes are opposite in sign and
reciprocals
(flip the number and change the sign )
6. Write the equation of a line: As soon as you see the words "FIND THE
EQUATION OF THE LINE ..."
WRITE DOWN the point-slope equation: 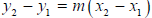
Find the slope if necessary, then substitute in a point and the slope.
7. Horizontal lines: Equation is of the form y = some constant (e.g., y =
1). Graph by making a t-chart by letting y = 1 for
several points, x can be anything! SLOPE IS 0.
8. Vertical lines: Equation is of the form x = some constant (e.g. x =
2). Graph by making a t-chart by letting x = 2 for several
points, y can be anything! SLOPE IS UNDEFINED.
9. Graph the solution to Linear Inequalities in two variables (example:
2x + 3y > 6):
(1) Graph the line (the =),
(2) Choose a dashed line for < , > solid line for ≤ , ≥ .
(3) Shade: Check a point in the inequality. If you get a true statement (like 0
< 5), shade the side containing the check
point. If you get a false statement (like 0 > 5), shade the OTHER side of the
line.
Topics from Chapter 4.
1. Solve two-variable systems of linear equations
Methods of solution : Elimination, Substitution, Graphing: The solution
you find by using substitution or elimination is the
intersection point when you graph the equations! ALL SOLUTIONS WILL HAVE BOTH AN
X AND A Y VALUE!! Once
you have solved for one variable, be sure to go back and solve for the other!!!
Graphing: Graph each line (use the checkerboard), find the point at which
they cross. This is the solution. CHECK IT in
each equation.
Substitution: solve for one variable in one equation, substitute into the
other.
Addition/ Elimination: multiply one or both equations to get opposite
coefficients on one variable. Add equations.
Types of systems :
Consistent (with one solution, two intersecting lines), Dependent
(with infinite solutions, one single line-variables drop
out, true statement) Inconsistent (with no solutions, parallel
lines-variables drop out, false statement)
2. Applications
Word problems using two variables: Interest, Money, Mixture and Solution
problems.
Interest and Money problems are alike. Mixture and Solution problems are alike.
On the latter, DON'T
FORGET to have the final percent or price per pound TIMES the final amount!!!
As always, DEFINE YOUR VARIABLES in words, set up and solve and equation and
ANSWER IN
WORDS.
Topics from Chapter 5:
1. Know the definition of exponents: 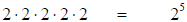
|
expanded |
exponential |
|
form |
form |
2. Apply the Properties of Exponentsin simplifying
expressions:
1. Product rule: 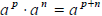 (add powers when
multiplying like bases)
(add powers when
multiplying like bases)
2. Quotient rule: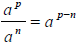 (subtract powers when
dividing like bases)
(subtract powers when
dividing like bases)
3. Power to Power rule: 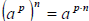 (multiply powers
when power to power)
(multiply powers
when power to power)
4. Distributive Property:
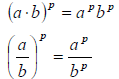
This DOESN'T work for addition!! I.e., 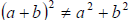
In working with exponents, IF IN DOUBT, EXPAND IT OUT.
5. Zero power rule: 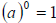
6. Negative power rule: 
(Negative exponents cause a “flip”; they NEVER result in a negative IN FRONT
of
the number!!!)
3. Polynomial expressions: Know the vocabulary:
Terms: the "clumps" separated by addition + and subtraction -
Coefficient: the number (not variable) in front of the term
Polynomial: Real number coefficients, variables raised to whole number
powers. No fractions with
variables in the denominator. No square roots with variables in them.
Degree of a term: highest power on variable in the term
Degree of the polynomial: Highest degree on any term
Monomial, Binomial, Trinomial: one, two , three terms, respectively
Like terms: same variables, same exponents on the variables.
Combine like terms: Add or subtract THE COEFFICIENTS ONLY. Leave the powers the
same!!!
Multiply polynomials: Distributive Property: Distribute each term in the first
polynomial to each term in the second.
FOIL: This is just a special case of the distributive property
Divide polynomials:
(1) by distributing: If there is a single term on the bottom, divide each term
in the numerator by it.
(2) by Long Division: If there is a polynomial with more than one term on the
bottom, use long division.
Remember: Divide, Multiply, Subtract (Change signs and add), Bring down and
repeat.
Chapter 6 Topics:
1. Factor Polynomials
Factoring:
A. Look for GCF first
B. Two terms: Difference of two squares (memorize this formula!)
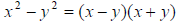
Sum or difference of two cubes (remember SOAP)
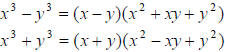
C. Three terms: Trinomial techniques (Split the middle or
Guess-and-check)
D. Four terms: grouping
2. Solve equations using factoring: Make equation = 0, factor completely, set
each factor = 0 and solve.
3. Solve Application problems: Including area problems and Freefall/projectile
problems.
11.2 Quadratic Equations
1. Solve a quadratic equation by
a. factoring (make equation = 0 first, THEN factor)
d. using the quadratic formula (put equation into standard form:
If 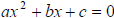 then
then
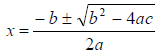
Chapter 10 topics: Roots and Radicals
1. Simplify radicals: The three criteria a radical must meet to be simplified
are
a. no perfect powers (power = root or a multiple of the root) under the radical;
i.e. no 2 of a kind in a square root, 3 of a kind in a cube root, etc.
b. no fractions should be under the radical (take the root of the numerator and
denominator separately)
c. no radicals in the denominator; Multiply bottom and top by “what’s missing”
to make 2 of a kind, 3 of a kind, etc.
(i) Rationalizing the denominator (SINLGE TERM): multiply numerator and
denominator by "what's
missing" under the radical in the given denominator. "What's missing" are the
factors needed to create a
perfect power (power = root or multiple of the root)
(ii) Rationalizing the denominator (TWO TERMS): Multiply numerator and
denominator by the
CONJUGATE of the denominator. Ex. Given 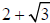 ,
the conjugate is
,
the conjugate is 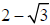
Be sure to simplify and reduce your final answer.
2. Combining radical expressions:
a. simplify all radicals as much as possible
b. identify like radicals (same radicand)
c. combine COEFFICIENTS in front of like radicals
3. Solving radical equations:
a. isolate radical, if possible (otherwise put one radical on each side of
equation)
b. raise both sides to power = root (for example: for a square root, square both
sides)
c. solve for x (linear equation: isolate x / quadratic equation: set = 0,
factor, set factors = 0)



