DECIMALS
Adding and Subtraction Decimals
|
Add: 28.5 + 44.47 + 3075.6 |
|
Subtract : 380.53 - 75 |
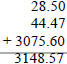 |
Step 1: Line up the decimal points. |
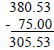 |
|
Step 2: Then add or subtract. |
Multiplying Decimals
Multiply 1.89 x 5.03 = ___
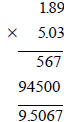 |
|
| |
| |
|
Step 1: Multiply the decimals as you would do
with whole |
Step 2:
Then count the number of spaces of each factor being multiplied. Decimal
places are the number of spaces to the right of the decimal point , There
is 2 in
the top factor and two in the bottom factor, so the decimal is placed 4
spaces
from the right. |
|
Step 3: Show the total number of places in
your answer. |
Dividing a Decimal by a Whole Number
Example:
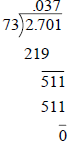 |
Place the decimal point directly above its position
in the problem.
Then divide the same way as you divide whole numbers. |
Dividing a Decimal by a Decimal Number
Example: 4.374 ÷ .03 = __
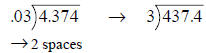 |
Move the decimal point of the divisor ( outside the
bracket ) as far right as you can
go. Then move the decimal point in the dividend (inside the bracket) the
same
number of places as the divisor. |
Place the decimal point directly above its position in the
problem. Then divide the same way as divide whole numbers.
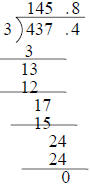
Practice:
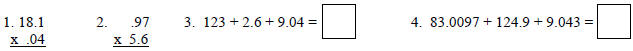
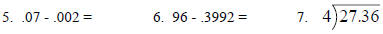

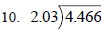
Answers:
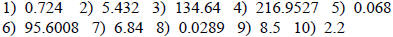
PERCENTS
Percents are used to describe a part of something. Percents are used to figure
out sales or the amount of interest someone will pay on a
loan. When converting a percent to its fraction form , it will always have a
denominator of 100.
Changing Decimals to Percents or Percents to Decimals
The important key is where to move the decimal point. If changing from
decimal to a percent , you would need to move the decimal
point two places to the right and add the percent sign .
Example:
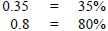
To change from percent to decimal, need to move the decimal point two places to
the left and drop the percent sign.
Example:
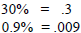
Converting Fraction to Percent Form
Divide the bottom number of the fraction into the top number and move the
point two places to the right.
Example: 
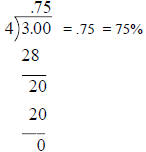
-or-
Multiply the fraction by 100%
Example: 
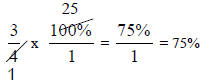
Percent to Fraction
Example: 85%
Percent of a Number
|
1) What is 25% of $6,500.
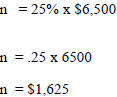 |
-or- |
2) Change the percent to a fraction
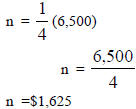 |
Finding What Percent One Number Is of Another
There are key words to remember that will help you solve the problem it is
asking you.
The word ‘of’ in the sentence means to multiply.
The word ‘is‘ means it is equal to.
Example:
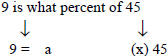 |
The variable ‘a’ is being multiplied by 45.
Need to divide by 45. |
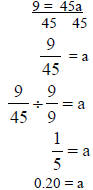
| |
20% = a |
Therefore, 20% of 45 is 9. |
Finding a Number When a Percent of It is Given
Example:
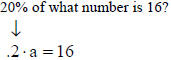
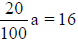 |
Change the percent to fraction form. |
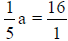
Practice:
Write the following in percent form.
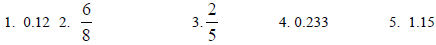
6. What is 11% of $3,000?
7. 60 is what percent of 12,000?
8. 28 is 40 % of what number?
Answers: