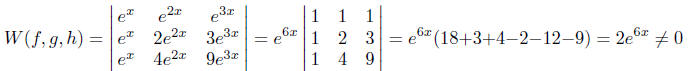General Solutions of Linear Equations

The general linear ordinary differential equation of order n has the form

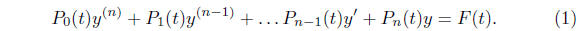
If we assume that 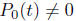on the interval I we can reduce this equation to
the form

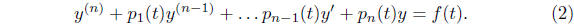
If the function f ≡ 0 we say that the equation (2) is homogeneous:

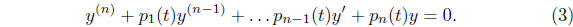
Theorem 1. Let 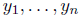be n solutions of the homogeneous linear equation
(3) on the interval I. If 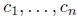are constants then the linear combination

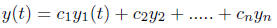
is also solution to equation (3).
.
The following theorem provide the existence and uniqueness result for the
initial value problem associated with the equation (2).

Theorem 2. Suppose that the functions 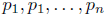and f are continuous
on the open interval I containing the ppoint a. Then, given n numbers
  the nth- order linear equation (2)

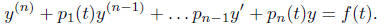
has a unique solution on the interval I that satisfies the n initial conditions

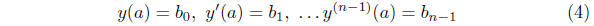
Definition. The n functions 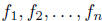are said to be linearly dependent
on the interval I provided that there exist constants 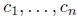not
all zero such that

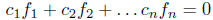
on I.
Suppose that 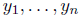are solutions to the homogeneous equation (3).
If they are linearly independent then the general solution to equation (3) is
given by formula :

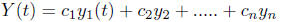
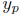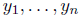Denote by some solution to equation (2). Let are linearly independent
solutions to homogeneous equation (3) . Then the general solution
to equation (3) is

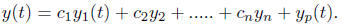
Example 1. Find a particular solution satisfying the given initial conditions

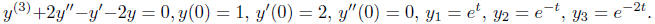
Solution. the general solution to the ordinary differential equation is

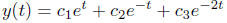
Let’s find the first and the second order derivatives of this solution

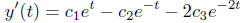
and

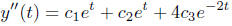
We have

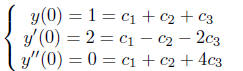
One can rewrite this system in the form

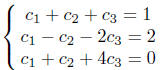
We subtract from the second and third equations the first one

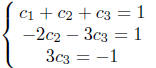
Therefore

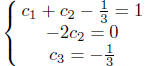
Finally we have

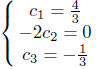
The solution to the initial value problem is

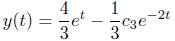
Example 2. Find a solution satisfying the given initial condition

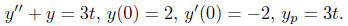
Solution. The general solution to the homogeneous ordinary differential
equation y '' + y = 0 is

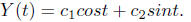
Hence the general solution to our equation is

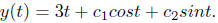
Taking the derivative of the function y'(t) we obtain

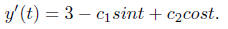
Then

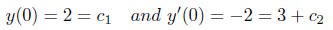
from the first equation we have

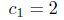
and from the second one

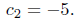
Hence the solution is

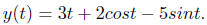
Example 3. Use the Wronskian to prove that functions f(x) = e^x, g(x) =
e^2x, h(x) = e^3x are linearly independent on the real line.
Solution.