Chapter 1: Introduction, Sec 1.1, 1.2, 1.3
1. Definitions:
(a) Differential Equation, Mathematical Model
(b) Direction ( Slope ) Field, Equilibrium Solution
(c) Rate (growth) constant
(d) Initial Condition, Initial Value Problem (IVP)
(e) General Solution, Integral curves
(f) Ordinary Differential Equation (ODE), Partial Differential Equation (PDE)
(g) Systems of Differential Equations
(h) Order, Linear, Nonlinear, Linearization
2. Important Skills:
(a) Derive differential equations that mathematically model simple problems.
(Example
1, p. 2; Also see p.7)
(b) Know what an initial value problem is, and how to show a given function is a
solution to one . (Example 2, p.13)
(c) Know the difference between an ordinary differential equation and partial
differential
equation. (p. 19)
(d) Know how to classify differential equations using order, and linearity.
(p.19-21)
Chapter 2: First Order Differential Equations, Sec 2.1, 2.2, 2.3,
2.4, 2.5, 2.6
1. Definitions:
(a) First Order Ordinary Differential Equation
(b) Integrating Factor , Integral Curves
(c) Separable differential equations
(d) Implicit solutions (p. 74)
(e) Logistic equations, intrinsic growth rate (p. 79)
(f) Existence and Uniqueness of Solutions, General Solutions,
(g) Autonomous, Logistic Growth, Equilibrium Solutions,
(h) Stable solutions, asymptotically stable solutions, unstable equilibrium
solution (p.
83)
(i) Threshold (p. 85)
(j) Critical Points (p. 88)
(k) Integrating factors, Exact equations (p. 94-98)
2. Theorems:
(a) Theorem 2.4.1: Existence and uniqueness of solutions to linear first order
ODE's.
(b) Theorem 2.4.2: Existence and uniqueness of solutions to first order IVP's
(c) Theorem 2.6.1: Existence and uniqueness of solutions to exact first order
ODE's.
3. Important Skills:
(a) Be able to determine if a first order differential equation is linear or
nonlinear .
Equation (3) on page 32 gives the form for a linear ODE.
(b) If the differential equation is linear, compute the integrating factor, and
then the
general solution (p. 36)
(c) If it's nonlinear, is it separable? If it's separable, you will need to
compute two
different integrals.
(d) If the differential equation is not separable, is it exact? If so, solve it
using the
method in Section 2.6 (Example 2, p. 97)
(e) It is crucial to know integration of basic functions and integral methods
from
your calculus course. For example, various substitutions, integration by parts,
and partial fractions will all be utilized.
(f) What happens to solutions as time tends to infinity? Understand stability,
asymptotic
stability and instability.
(g) Understand the three steps in the process of mathematical modeling:
construction
of the model, analysis of the model, and comparison with experiment or
observation. (Example 1 p. 52)
(h) Understand Relevant Applications: Mixing Problems, Compound Interest .
(i) Determine the existence and uniqueness of solutions to differential
equations.
(Examples on p. 70-75)
(j) Know how to recognize autonomous equations, and utilize the direction field
to
represent solution to them. Be able to determine asymptotically stable,
semistable,
and unstable equilibrium solutions. (Example 1, p. 83)
(k) Know the concept of a threshold value (Section 2.5)
Chapter 3: Second Order Linear Equations, Sec 3.1, 3.2,
3.3, 3.4,
3.5, 3.6, 3.7
1. Definitions:
(a) Linear vs. nonlinear
(b) Homogeneous vs. nonhomogeneous
(c) Characteristic Equation, Wronskian
(d) Principle of superposition (p. 145)
(e) Linear Independence and dependence
(f) General Solution, Fundamental Set of Solutions
(g) Particular Solution
(h) Method of undetermined coefficients
(i) Method of variation of parameters
2. Theorems:
(a) Theorem 3.2.1: Existence and uniqueness of solutions to
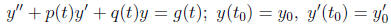
(b) Theorem 3.2.2: Principle of superposition. If
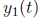 and
and 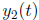 are
solutions to (2),
are
solutions to (2),
so is 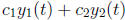 for any constants
for any constants
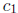 and
and 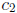 .
.
(c) Theorem 3.2.3: Finding solutions to initial value problems using the
Wronskian
at the initial conditions.
(d) Theorem 3.2.4: Representing general solutions to second order linear
homogeneous
ODE's
(e) Theorem 3.3.1: Linear independence of functions and the Wronskian.
(f) Theorem 3.3.2: Abel's Theorem.
(g) Theorem 3.3.3: "Let 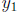 and
and
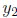 be two solutions of Eq. (7)." Linear
independence
be two solutions of Eq. (7)." Linear
independence
of solutions to y" + p(t)y' + q(t)y = g(t) and the Wronskian.
(h) Theorem 3.6.1: Relating differences in nonhomogeneous solutions to
fundamental
solutions (Used to prove the following theorem.)
(i) Theorem 3.6.2: General solutions to linear nonhomogeneous ODE's.
(j) Theorem 3.7.1: General solutions to linear nonhomogeneous ODE's. (Using
variation
of parameters to determine the particular solution.)
3. Important Skills:
(a) Be able to determine if a second order differential
equation is linear or nonlinear,
homogeneous, nonhomogeneous. (If it can be put into the form given by Equation
(3) in page 136, it is linear.)
(b) Can you recognize a homogeneous equation with constant coefficients, and
derive
the characteristic equation? (Example 3, p.147) This equation will be quadratic,
so know the quadratic formula , the types of solutions one gets; real and
distinct,
repeated, and complex conjugate . These three cases will be crucial to the types
of solutions one gets to constant coefficient homogeneous differential
equations.
(c) Be able to write down fundamental solution sets to homogeneous equations.
This
means find two linearly independent solutions. You can use the Wronskian to
show if two solutions are linearly independent. (Example 3, page 147). Many
times the Wronskian is the most convenient method to determine dependence.
(d) What are the fundamental solution sets for each of the three case of roots
when
solving constant coefficient equations? The summary is on p . 170. (Example 3,
p.147; Example 2, p.162; Example 2, p.169)
(e) Reduction of order is a way to take a known solution and produce a second
linearly
independent one (Example 3, p.171).
(f) Solutions to second order nonhomogeneous equations have two components.
There
is the homogeneous solution, and particular, or nonhomogeneous solution (Theorem
3.6.2, p.176). To find particular solutions you must know the method of
undetermined coefficients, and variation of parameters. (Example 4, p. 179;
Example 1, p. 186)
Chapter 4: Higher Order Linear Equations, Sec 4.1, 4.2, 4.3, 4.4
1. Definitions:
(a) n-th Order Linear ODE
(b) Fundamental Set of Solutions, General Solution
(c) Homogeneous and Nonhomogeneous Equations
(d) Linear Dependence and Independence
(e) Characteristic Polynomial, Characteristic Equation
(f) Undetermined Coefficients
(g) Variation of Parameters
2. Theorems:
(a) Theorem 4.1.1: Existence and uniqueness of solutions to higher order linear
ODE's.
(b) Theorem 4.1.2: General solutions to higher order
linear ODE's and the fundamental
set of solutions
3. Important Skills:
(a) The methods for solving higher order linear differential equations are
extremely
similar to those in the last Chapter. There is simply n times the fun! The
general
solution to an n-th order homogeneous linear differential equation is obtained
by
linearly combining n linearly independent solutions. (Equation 5, p. 220)
(b) The generalization of the Wronskian is given on page 221. It is used as in
the last
Chapter to show the linear independence of functions, and in particular
homogeneous
solutions.
(c) For the situation where there are constant coefficients, you should be able
to
derive the characteristic polynomial, and the characteristic equation, in this
case
each of n-th order. Depending upon the types of roots you get to this equation,
you will have solution sets containing function similar to those in the second
order
case. (Examples 2-4, p. 227-229)
(d) The general solution of the nonhomogeneous problem easily extends to the n-th
order case. (Equation 9, p. 222)
(e) Both variation of parameters, and the method of undetermined coefficients
generalize
to determine particular solutions in the higher dimensional situation. (Example
3, p. 234; Example 1, p. 239)
Chapter 6: The Laplace Transformation, Sec 6.1, 6.2, 6.3, 6.4
1. Definitions:
(a) Laplace Transform, Kernel
(b) Improper Integral
(c) Piecewise Continuous function
(d) Unit Step Function (Heaviside Function)
2. Theorems:
(a) Theorem 6.2.1: Laplace Transform of f '(t)
(b) Corollary 6.2.2: Laplace Transform of 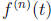 for n = 2.
for n = 2.
(c) Theorem 6.3.1: Transform of the unit step function,
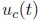 , times a shifted function,
, times a shifted function,
f(t - c)
3. Important Skills:
(a) The Laplace transformation is defined through an
improper integral. You must be
comfortable evaluating them. Hence you should review this topic in any calculus
book.
(b) Be able to calculate the transform of all the basic functions, given in the
table 6.2.1
on page 319. (Examples 5, 6 & 7, p.311-312) However, the table will be given
to you in the exam. You should be able to use the table to calculate Laplace
transforms and inverse Laplace transforms.
(c) Even more importantly, know how to compute inverse transform functions using
manipulative translation methods. You may need to use partial fractions, but
you should have already reviewed this for Chapter 2. (Examples 1 & 2, p.320)
(d) Know how to transform derivatives of functions and linear differential
equations.
(Theorem 6.2.1 and Corollary 6.2.2, Examples 1 & 2, p.320)
(e) Understand the unit step function, 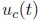 , and
how to use them in transforming
, and
how to use them in transforming
and inverse transforming functions. (Example 2, p.335). Also, solve initial
value
problems in which the forcing function is a step function or a translated
(piecewise
continuous) function. )
(f) The process of using the Laplace transform method is as follows; Given a
differential
equation, one transforms both sides of the equation. One will need to
input the initial values when transforming derivatives. Derivatives with respect
to t transform to polynomials in s . If the differential equation is linear, then
the
resulting equation is linear in Y (s). You simply solve the equation for Y(s),
and
then use all the methods available to invert the Laplace transform and recover
y(t). (Example 1, p.320 for continuous forcing; Example 2, p.335 for
discontinuous
forcing.)



