In addition to the forms of quadratic expressions already
addressed in part 1, there are
some other special forms of quadratic equations that present special cases when
factoring.
When c = 0:
When c = 0, factoring is much simpler. In this case, you have an equation of the
form
ax2 + bx = 0.
To factor the expression on the left hand side in this case, you simply factor
out any
common factor between a and b, and the common x. This results in an expression
that
looks like hx ( kx + l ) where h is the common factor from a and b, and k and l
are the
factored coefficients . This is the final factored form, and from here, the
equation is ready
to solve.
Example 1:
Factor the expression 4x2 + 6x.
Solution:
1. The greatest common factor of 4 and 6 is 2, so factor a 2 and an x from each
term.
2. We now have the expression 2x (2x + 3), which is the solution.
Difference of Squares
Another case when factoring quadratic expressions is called the Difference of
Squares.
This occurs when the expression is the difference of two squares . When this is
the case,
we have an expression of the form ax2 + c, which factors into an
expression of the form
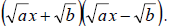
The two squares do not necessarily have to be perfect squares (such as 4, 9, 16
…) since
it is possible to leave a radical in the final answer, but it is often the case
that the factors
are perfect squares.
Example 2:
(a) Factor the expression 16x 2 −9.
(b) Factor the expression 3x 2 − 7 .
Solutions:
(a) 16 and 9 are both perfect squares, so the square roots are 4 and 3,
respectively.
Next, setting up the factored expression in the form shown above, the expression
is
(4x + 3)(4x − 3).
(b) In this case, 3 and 7 are not perfect squares, but their square roots may be
represented by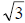 
and
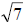. From this point, the factored expression takes the form
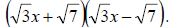
Similarly, it is not necessary to have an x2 term. Observe
in the next example what
happens when an x4 term or an x term exists in place of the x2 term. Notice that
as long as
it is the difference of two terms, the square root of each term is used in
factoring,
regardless of whether or not it is a perfect square.
Example 3:
(a) Factor the expression x – 25.
(b) Factor the expression x4 – 36.
Solutions:
(a) First, notice that the original expression is already in factored form. For
solving
many equations, it is unnecessary to factor this expression any further.
However, in
some cases it may be useful to factor this expression as a difference of
squares,
especially when simplifying certain types of expressions. So, we will take the
square
root of each term. The square root of x is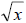
and the square root of 25 is 5. So,
setting up our parenthesis, and placing each part in its place, we have the
expression
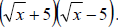This is the final solution.
(b) In this case, the expression is clearly not in factored form. First, take
the square
root of each term. In this case,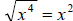
and
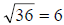. So, setting up the
parentheses, we have the expression (x2 + 6)(x2 − 6). Now, notice that the
second
factor, (x2 – 6) can be factored further as a difference of squares. Factoring
that
expression as we did the expressions in Example 2, we now have our final
expression,
which is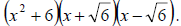 
Solving Quadratic Equations By Factoring
Once an expression has been factored, the resulting expression may be used to
solve
quadratic a equation. A quadratic expression, which is what this tutorial has
focused on
so far, is one part of a quadratic equation. A quadratic equation, in standard
form looks
like ax2 + bx + c = 0. It is important that the right hand side be zero in order
for this and
other methods of solving quadratic equations to give the correct solution.
Once the equation has been factored, it is possible to find the two possible
solutions to
the quadratic equation. Remember that the factored form of a quadratic
expression is
(hx + m) (kx + n).
So the factored quadratic equation is (hx + m) (kx + n) = 0. Now, since the
factors are
multiplied, only one needs to equal 0 in order for the whole left hand side to
equal 0,
since anything multiplied by 0 equals zero. So set each factor equal to 0
individually and
solve for x. Lets look back at some of the examples from part 1 and part 2 and
solve
them.
Example 4:
Solve the equation x2 – 5x + 6 = 0 for x.
Solution: In Part 1, Example 2, we showed that the
factored form of the left hand
side of this equation was (x – 2)(x – 3). So now the
equation is (x – 2)(x – 3) = 0.
Remember that to solve for x, it is necessary to set each factor equal to 0, one
at a
time, and the two results will be the two solutions. So we now have two
equations:
x – 2 = 0 and x – 3 = 0.
The solution to these two equations are x = 2 and x = 3 respectively, and so
these are
the two solutions to the equation.
Example 5:
Solve the equation 4x2 + 6x = 0 for x.
Solution: The expression on the left hand side of this equation was factored in
Example 1 of part 2, with the result 2x (2x + 3), so our equation is now
2x (2x + 3) = 0.
Setting each expression equal to 0, we have 2x = 0 and (2x + 3) = 0. These two
equations give the results x = 0 and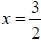 
respectively.
Example 6:
Solve the equation 16x2 −9 = 0 for x.
Solution: The expression on the left hand side in this case is a difference of
squares,
and was factored in Example 2a of part 2. The factored result in this case was
(4x + 3)(4x − 3), so the equation is (4x + 3)(4x −3) = 0 . Setting each factor
equal to
zero and solving , we have (4x + 3) = 0 and (4x − 3) = 0 with solutions of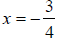
and
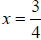respectively. Notice that the solutions are the same with opposite sign.
This
will always be the case when solving a difference of squares quadratic equation.
It will not always be possible to solve a quadratic equation by factoring, since
every
equation is not factorable. In this event, one of the methods described in other
tutorials
may be used.
