Projection Methods for Linear Equality Constrained
Problems
1 Review of Steepest Descent
Suppose we want to solve
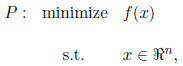
where f(x) is differentiable . At the point
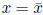, f(x) can be approximated
by its linear expansion
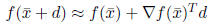
for d “small.” This leads to the choice of d dictated by
the direction-finding
problem:
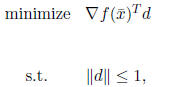
which is equivalent to :
The solution to this direction finding problem is:
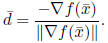
Because we choose our next step as
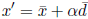
for some choice of step-length α, then we can re-scale the
direction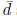 
simply
as:
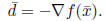
That is, the steepest descent direction is simply the
negative of the
gradient of f(x) at .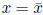
2 Equality Constrained Problems
Now consider the slightly more complicated problem
P : minimize f(x)
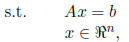
where f(x) is differentiable . The KKT conditions for this
problem are as
follows:
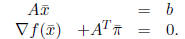
We wish to find such a KKT point.
Suppose that we are at the point
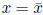, where,
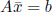, i.e., 
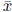is a feasible
point. Again we have
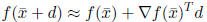
for d “small.” In order to choose the direction
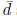and compute the next
point
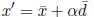
for some stepsize α, we will solve the following
direction-finding problem:
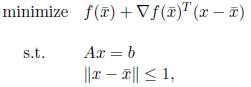
or equivalently (by setting
)
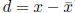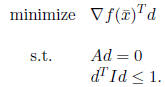
Note that Ad = 0 ensures that
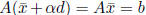for any α. Also note
that the constraint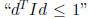 
says that d must lie in
the Euclidean unit
ball B, defined as:
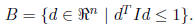
However, the Euclidean ball is but one metric, and we
might instead be
more general, and choose to restrict d to lie in an ellipsoid
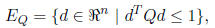
where Q is a given symmetric and positive -definite matrix.
This leads to the
more general direction-finding problem:
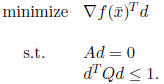
The projected steepest descent algorithm is:
Step 1.
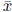satisfies 
.
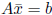Compute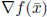
.
Step 2. Solve the direction-finding problem (DFP):
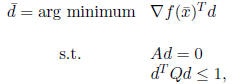
If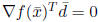 
, stop . In the
case ,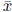 is a Karush-Kuhn-Tucker
point.
Step 3. Solve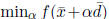 
,for
the stepsize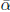 
, perhaps chosen by an exact
or inexact linesearch.
Step 4. Set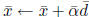 
. Go to Step 1.
Note that if Q = I and the equality constraints Ax = b are absent, this
algorithm is just the steepest descent algorithm.
3 Properties of the Projected Steepest Descent
Direction
Note that DFP is a convex program, and d = 0 is a Slater point. Therefore,
the Karush-Kuhn-Tucker conditions are necessary and sufficient for
optimality in DFP. These conditions are:
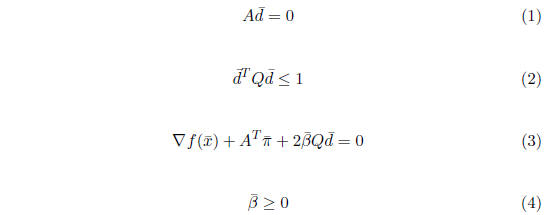
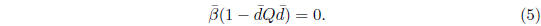
As it turns out, it is extremely easy to solve these
equations . (We will
see this shortly.) Let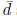
solve the equations (1)-(5) with multipliers 
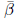and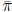 
.
Proposition 3.1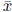
is a Karush-Kuhn-Tucker point of P if and only if
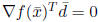
Proposition 3.2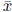
is a Karush-Kuhn-Tucker point of P if and only if
=
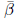0.
Proposition 3.3 If
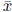is not a Karush-Kuhn-Tucker
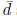point of P, then is
a descent direction.
Proposition 3.4 The projected steepest descent algorithm has the same
convergence properties and the same linear convergence as the steepest descent
algorithm. Under the same conditions as in the steepest descent algorithm,
the iterates converge to a Karush-Kuhn-Tucker point of P, and the
convergence rate is linear, with a convergence constant that is bounded in
terms of eigenvalues identically as in the steepest descent algorithm.
