1 Arithmetic
§1. Here are some things which should be easy for you. (If they are not,
you
may not be ready for calculus.)
1. Factor x 2 − 6x + 8.
2. Find the values of x which satisfy x2 − 7x + 9 = 0. (Quadratic formula.)
3. x2 − y2 =? Does x2 + y2 factor?
4. True or False: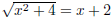
?
5. True or False: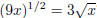 
?
6. True or False: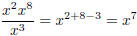 
?
7. Which x satisfy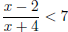 
?
8. Find x if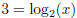 
.
9. What is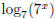 
?
10. True or False: log(x + y) = log(x) + log(y)?
11. True or False: sin(x + y) = sin(x) + sin(y)?
§2. There are conventions about the order of operations. For example,
ab + c means (ab) + c and not a(b + c),
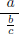means a/(b/c) and not (a/b)/c,
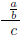means (a/b)/c and not a/(b/c),
log a + b means (log a) + b and not log(a + b).
If necessary, we use parentheses to indicate the order of
doing the operations.
§3. There is analogy between the laws of addition and the laws of
multiplication:
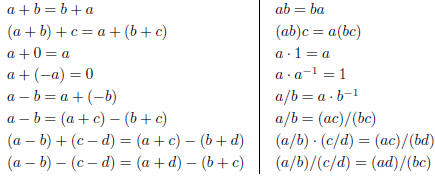
The last line explains why we invert and multiply to
divide fractions. The only
other law of arithmetic is the distributive law
(a + b)c = ac + bc, c(a + b) = ca + cb.
Note that
(a + b)/c = (a/c) + (b/c), but c/(a + b) ≠ (c/a) + (c/b).
2 Polynomials and Rational Functions
§4. A polynomial is a function of the form
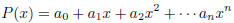
where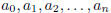 
are constants. When
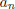≠ 0 we say the polynomial
has
degree n. Thus
P(x) = 3 + 7x + 2x5
is a polynomial of degree 5. A rational function is a ratio of two polynomials
like
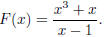
When (as in the example) the degree of the numerator is greater than or equal
to the degree of the denominator, you can do long division and write
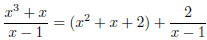
which expresses the rational function as a polynomial plus another rational
function where the degree of the numerator is smaller than the degree of the
denominator. In other words
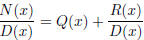
where N(x), D(x), Q(x), R(x) are polynomials and the
degree of the remainder
R(x) is smaller than the degree of the denominator D (x). We can multiply both
sides by D(x) to get
N(x) = Q(x)D(x) + R(x), degR(x) < degD(x). 
§5. When the denominator D(x) is of degree one it has the form D(x) = x−a.
Then the remainder R(x) will be a constant r so formula
takes the form
N(x) = Q(x)(x − a) + r.
If we plug in x = a we get N(a) = Q(a)(a − a) + r = 0 + r = r so
N(x) = Q(x)(x − a) + N(a).
Of course when N(a) = 0 the last formula is N (x) = Q(x)(x − a). This proves
the important principle
A polynomial N(x) vanishes at x = a
if and only if it is divisible by x − a.
§6. For example,
x3 + 3x − 2 = (x2 + x + 4)(x − 1) + 2
and x3 + 3x − 2 = 2 when x = 1. Similarly, x3 + 3x − 4 = 0 when x = 1 so
x3 + 3x − 4 is evenly divisible by x − 1. If you do the long division, you get
x3 + 3x − 4 = (x2 + x + 4)(x − 1).
3 Coordinate Geometry
The following material is crucial for understanding calculus. It is
reviewed in sections 1-1 through 1-6 but if you have not seen it before
you may not be ready for calculus.
§7. The notation P(x, y) is used as an abbreviation for the more cumbersome
phrase “the point P whose coordinates are (x, y).” The slope of the line through
the distinct points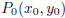 
and
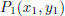is
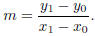
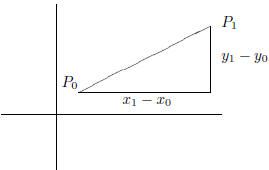
§8. If we use a different pair of points on the line to
compute the slope, we get
the same answer (see page A12 of the text). Hence, a point P(x, y) lies on the
line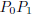 
if and only if we get the same answer for the slope when we use (x, y)
in place of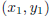 
:
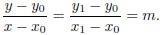
This equation has one minor flaw; it doesn’t work when
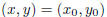(never
divide by zero ). To remedy this multiply by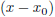 
and add
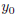to both sides:
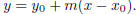
This is the equation for the line through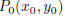 
with slope m; this form
makes
it obvious that the point 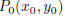lies on the line. For example, the equation
for the line through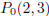 
and
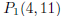is
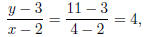or or y = 3 + 4(x − 2)
