Subtraction of Fractions
When subtracting mixed numbers, you may need to “borrow” a whole number to
subtract the fractions.
Example:
5 1/5 - 2 3 /10 = _______________
Step 1: Convert the fractions with unlike denominators (bottom numbers)
to
fractions with the same denominator.
5 1/5 - 2 3/10 =
5 2/10 - 2 3/10 =
Step 2: Before we can subtract the fractions, we must borrow 1 (10/10)
from the 5.
5 2/10 - 2 3/10 =
4 12/10 - 2 3/10 =
Step 3: Separate the whole numbers and fractions.
4 12/10 - 2 3/10 =
Step 4: Subtract the whole numbers.
4 - 2 = 2
Step 5: Subtract the fractions.
12/10 - 3/10 = 9/10
Step 6: Combine the results.
Therefore: 5 1/5 - 2 3/10 = 2 9/10
Skill Check
21. 2 2/3 - 1 ¾ = _______________
22. 8 7/20 - 2 ¾ = _______________
23. 9 1/6 - 3 8/9 = _______________
24. 4 ½ - 2 5/16 = _______________
25. 16 ¼ - 7 5/8 = _______________
Multiplication of Fractions
To multiply with mixed numbers, first you must change the mixed numbers into
improper fractions.
Steps for changing mixed numbers to improper fractions:
Step 1: Find the product of the denominator of the fraction and the whole
number.
Put the product over the denominator.
Step 2: Add the two fractions.
Example: Change 3 2/3 into an improper fraction.
Step 1: Multiply the denominator (3) by the whole number (3). Put the
product (9)
over the denominator (3).
Step 2: Add the two fractions.
3 2/3 = 9/3 + 2/3 = 11/3
To multiply one or more mixed numbers, the first step is to change all to
improper
fractions.
Steps for multiplying mixed numbers:
Step 1: Change every mixed number into an improper fraction.
Step 2: Add the fractions.
Example: Multiply 2¾ × 1/3
Step 1: Change 2 to an improper fraction. 2 = 8/4
Step 2: Add 8/4 and ¾ = 11/4
(2¾ = 2 + ¾ = 8/4 + ¾ = 11/4)
Step 3: Multiply the improper fraction from Step 2 (11/4) by the other
fraction
(1/3).
11/4 × 1/3 = 11/12
Note: Multiply the whole number by the denominator and add the numerator .
|
denominator |
whole number |
numerator |
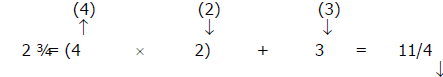 |
| |
denominator remains the same (4) |
Skill Check
Multiply the following mixed numbers:
26. ¾ × 1¼ = _______________
27. 3 × 4½ = _______________
28. 2¾ × 3 4/5 = ______________
_
29. 4 1/3 × 3 4/5 = _______________
30. 6 1/3 × 4 = _______________
Division of Fractions
Dividing fractions is simply finding out how many times one number will go into
another
number. Dividing fractions take it one step further than multiplying fractions.
Steps for dividing fractions:
Step 1: To divide by a fraction, multiply by its reciprocal (invert the
divisor the
number you’re dividing by). Turn the fraction upside down. Before you can
divide, you must find the reciprocal . Before you can change to its reciprocal,
invert the divisor. You must first change it to a fraction if it’s not one
already.
Step 2: Change the division sign to multiplication.
Step 3: Multiply to get the answer.
Steps for dividing fractions by fractions:
Step 1: To divide by a fraction, multiply by its reciprocal. Find the
reciprocal of the
fraction you are dividing by (the divisor) and multiply.
Step 2: Invert the fraction (divisor)
Step 3: Change the division sign to multiplication.
Step 4: Multiply
Example: Divide 7/8 by 2/3
Skill Check
31. 3/6 ÷ 1/3 = _______________
32. 7/8 ÷ ½ = _______________
33. 1/3 ÷ 3/8 = _______________
34. 2/3 ÷ 2/3 = _______________
35. 2/3 ÷ 1/2 = _______________
Now select your area of work and then turn to the
appropriate page for “Let’s Apply to
Your Workplace” questions:
Nursing Assistant ---------------------- Page 137 - 138
Dietary Services ----------------------- Page 139 - 140
Environmental Services --------------- Page 141 - 142
Let’s Apply to Nurse Assistant
Mathematics – Lesson 6 of 7
Nursing assistants use fractions in many different places . An example would be
calculating the amount of a meal a resident has consumed. Nursing assistants
must
determine the fractional portion consumed and then record the amount on the
resident’s chart.
Example
Ellie May is one of the residents that you are responsible for. You are to chart
the
amount of solid food that Ellie May consumes. For the noon meal today she ate
1/2 of
a 3-ounce serving of meat loaf and 3/4 of her 3-ounce serving of mashed potatoes
and
1-ounce serving of gravy. She also ate 1/3 of a 2-ounce serving of green beans
and
one slice (1 ounce) of bread. How many ounces of solid food did Ellie May
consume?
| Meat loaf |
1/2 of a 3 oz. serving |
1/2 × 3 = 3/2 = 1 1/2 oz. |
| Mashed potatoes |
3/4 of a 3 oz. serving |
3/4 × 3 = 9/4 = 2 1/4 oz. |
| Gravy |
3/4 of a 1 oz. serving |
3/4 × 1 = 3/4 oz. |
| Green beans |
1/3 of a 2 oz. serving |
1/3 × 2 = 3/2 = 1 1/2 oz. |
| Bread |
all of a 1 oz. serving |
1 oz. |
1 1/2 + 2 1/4 + 3/4 + 1 1/2 + 1 =
3/2 + 9/4 + 3/4 + 3/2 + 1 =
6/4 + 9/4 + 3/4 + 6/4 + 4/4 = 28/4 = 7 ounces of solid food consumed
Exercise
1. You are assisting the in-charge nurse preparing medications that will be
administered to the residents this evening. If she has a supply of 17 1/2 ounces
of a particular medication, and each resident’s dose is 1 1/4 ounces, how many
residents will the in-charge nurse be able to administer a proper dose to?
Answer: ___________________________
2. You are a medication aid and are required to administer 26 doses of a
medication
of which you need 1 1/3 ounces per dose. If you only have one 32-ounce bottle of
the medication on hand, how many doses will you be able to administer?
Answer: ___________________________
Is there enough medication on hand to administer a dose to each of the 26
residents?
Answer: ___________________________
3. You are responsible for charting the liquid intake of one of the residents on
your
floor. During your shift the resident had a 6-ounce glass of juice, but only
drank
2/3 of it. In addition, he drank 3/4 of an 8-ounce cup of coffee. He also had 12
1/2 ounces of water. How many ounces of liquid did he consume during your
shift?
Answer: ___________________________
Let’s Apply to Dietary Services
Mathematics – Lesson 6 of 7
Dietary Services workers use fractions in many different places. An example
would be
calculating the amount of an ingredient required when a recipe is being doubled
or
tripled. Dietary Services workers must determine the correct fractional amounts
required so that each batch will turn out properly.
Example
Your supervisor has instructed for you to make 15 apple pies for tomorrow’s
deserts.
You review the recipe and see that each pie requires 1 1/4 teaspoons of
cinnamon.
When you check the supplies, you discover that the cinnamon container is almost
empty
and find out that more cinnamon is on order , but will not be delivered until
tomorrow.
You measure the cinnamon that you have on hand and determine that there is 12
1/2
teaspoons full. How many apple pies will you be able to make?
12 1/2 ÷ 1 1/4 =
25/2 ÷ 5/4 =
25/2 × 4/5 = 100/10 = 10There is enough cinnamon on hand
to make up 10 apple pies.
Exercise
1. You are preparing a drink mix for the evening meal. The instructions say to
use
3/4 cup of sugar for each gallon of drink you are mixing and your instructions
say
to make up 4 1/2 gallons of drink. How much sugar will you need?
Answer: ___________________________
2. You are making the deserts for the evening meal. You are to make up three
sheet
cakes and a double batch of cookies. How much cooking oil will you need if each
cake requires 2 1/4 cups and each batch of cookies requires 1 1/3 cups of oil?
Answer: ___________________________
3. You are to make up a large batch of vegetable soup for tomorrow’s lunch. The
recipe says to add 2 1/2 cups of beef stock for each 1/2 gallon of soup. How
much beef stock will you need if you are making 5 gallons of vegetable soup?
Answer: ___________________________
Let’s Apply to Environmental Services
Mathematics – Lesson 6 of 7
Environmental Services workers occasionally use fractions in their workplace. An
example would be calculating the correct amount of disinfecting concentrate to
be
added to water to make up a cleaning solution.
Example
You are to mix up a bucket of disinfecting solution and wash down the walls and
floors
of the showers in both the men and women’s bathrooms. The directions on the
container of disinfecting concentrate say to add 1/3 cup of concentrate to each
quart of
water. How much concentrate will you need to add to 5 1/4 quarts of water to
obtain
the proper mixture?
1/3 × 5 1/4 =
1/3 × 21/4 = 21/12 = 1 9/12 = 1 3/4 cups of concentrate
Exercise
1. You are preparing to strip and re-wax the main hall floor. The directions on
the
stripper concentrate say to mix 1 1/2 cups of the concentrate with each gallon
of
warm water. If you have 5 gallons of water, how many cups of stripper
concentrate will you need to add to have the proper stripping solution?
Answer: ___________________________
2. You are assigned to work in the laundry area today to fill in for an employee
who
is off sick. The automatic soap dispenser on the washing machine is not working
and you are told to measure and add 2/3 cup of soap powder to each load that
you run. How many cups of soap powder will you need to wash 9 loads of bed
linens ?
Answer: ___________________________
3. You have the assignment of mixing up a disinfecting solution and then washing
down the walls, furniture and floors in one of the rooms. The directions for
mixing the solution say to add 1/4 cup of bleach to each 1 1/2 quarts of water.
If
you have 4 1/2 quarts of water in a bucket, how many cups of bleach should you
add to have the proper mixture?
Answer: ___________________________



