Introduction
The number zero is a very powerful tool in mathematics that has many different
applications and rules . An interesting fact about the number zero is that
according to our calendar
(the Gregorian calendar), there is no “year zero” in our history. There is also
no “zeroth” century
as time is recorded from centuries B.C. to the 1st century A.D. However, certain
calendars do
have a year zero. In the astronomical year numbering system year zero is defined
as year 1 BC.
Buddhist and Hindu lunar calendars also have a year zero. In this paper I am
going to discuss
many different uses of the number zero in mathematics and in the world. I am
also going to
discuss the origins of the number zero.
Zero as a Numeral
I learned from Wikipedia, the word zero comes from the Arabic translation of the
Sanskrit sunya, around 400 B.C. in India. Sunya means void or empty. The Romans
translated
the word between the 5th and 1st century B.C. using Latin
to become zephyrus which meant “west
wind”. The word zephyr is used today to mean a light breeze. Fibonnaci, a famous
Italian
mathematician, who lived from 1170 to 1250, introduced this concept to Europe
and the word
became zefiro in Italian, and was then changed to zero in the Venetian dialect.
The actual
symbol 0 that we use was developed in India in the 9th century A.D.
The number zero is an important number because it serves
as a place holder to help
distinguish the difference between numbers like 230 and 23. The ancient
Babylonians, who used
a base 60 system, did not have zero as a placeholder, but instead used a
separator mark to
separate places. The Babylonians had 59 different numbers that fit into a single
position. Each
number consisted of a different combination of symbols. The first position from
the right is the
600 or units place, the next place to the left is the 601
place, and so on through 60n. The number
8 32 would be 8 × 601 + 32 × 600 which would be 480 + 32
which equals 512. The base 60
system is still used in our society today through the way that we measure time
(sixty seconds in a
minute, sixty minutes in a hour) and the way that we measure the degrees in a
circle.
Numbers with Many Zeros
A googol is defined as10100, which can be written as a 1 followed by
100 zeros. It can
also be obtained by taking 1 million to the 16th power and then
multiplying that result by ten
thousand. On Wikipedia, I found the term googol was coined in 1920 by a nine
year old named
Milton Sirotta, the nephew of a famous mathematician named Edward Kasner. A
googol has
only two prime factors, they are 2 and 5 and there are 100 of each of them.
There are many names for very large numbers that I found while looking through
at the
online encyclopedia called Wikipedia. I learned that a quadrillion is 1015,
an octillion is 1027 , a
googolplex is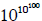 
and there are many more names
for very large numbers that are not listed
here. An example of an amount that is in the quadrillions is the number of BTU’s
that were used
in the United States in 2002 according to the United States Department of
Energy. Because it is
so difficult for most people to grasp numbers this large, the names for numbers
larger than
quadrillion are not commonly used . Instead, large numbers are more commonly
expressed in
scientific notation. Large numbers which must be written in scientific notation
can be found in
RSA codes, distances in outer space, and genome structure.
Length and Dimension Zero
In geometry a point is defined to have a dimension of zero while a line or line
segment
has dimension 1. A plane is 2-dimensional by definition.
Division by Zero : Undefined, indeterminate, or infinity
Division by zero is undefined. The reason for this is made clear by examining
the inverse
of division, namely, multiplication. Every division statement can be written as
a corresponding
multiplication statement. For example 6 ÷ 3 = 2 corresponds to 2× 3 = 6 .
Suppose we state that
5 ÷ 0 = 0 , then the corresponding multiplication statement gives 0× 0 = 5 ,
which is clearly a
false statement. Thus, 5 ÷ 0 ≠ 0 and it follows that x ÷ 0 ≠ 0 for any nonzero
x. Now suppose
that 5 ÷ 0 = n for some n. Then n must satisfy 0× n = 5 . However, by the
multiplicative property
of zero, the product of any number times zero is equal to zero. In general, if x
÷ 0 = n then this
implies that 0× n = x . For nonzero x there is no value of n which makes this
true, so that x ÷ 0 is
undefined. If x = 0 we see that 0 ÷ 0 is indeterminate, because 0× n = 0 for any
n.
It is possible to divide zero by a non-zero number. For example, 0 ÷ 8 = 0
corresponds to
0 = 8× 0 which is not a contradiction.
Sometimes students in upper level mathematics might be taught that a number
divided by
zero is infinity. This is a reasonable statement if their teacher explains that
the zero in the
denominator represents numbers that approach zero (and are positive). Dividing a
number by
(positive) numbers which get smaller and smaller, produces values which get
larger and larger
and approach infinity.
Different Algebraic Expressions with Zero
It is very interesting to examine the role of zero in different algebraic
expressions. The
expression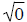 
is a valid expression because 02
= 0× 0 = 0 . Similarly the expression 
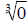is
valid because 03 = 0× 0× 0 = 0 . The expression x0 is
valid because any non-zero real number
raised to the zero power is defined as 1. 00 is an interesting
special case of x0 because a lot of
people will look at 00 and think that the answer is 0. As I learned
from a website named Ask Dr.
Math, 00 is said to be an indeterminate form. This means in some
cases we think about it as
having one value, and in other cases we say it has a different value. Setting 00
equal to 1 lets
mathematicians use definitions in other areas of mathematics without having to
make special
cases for 0. A concept where having 00 = 1 is useful is when using
the binomial theorem. 0x is
a valid algebraic expression because the exponent x tells you how many times to
write the base 0.
No matter how many times you multiply zero by itself the product is always zero.
Recall that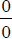 
,
or 0 ÷ 0 , is an indeterminate form (see previous discussion). A good example of
why 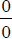is an
indeterminate form can be found on the Ask Dr. Math website. If you evaluate the
limit of the
expressions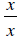 
and
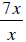as x approaches zero, although substituting
zero in for x demonstrates
that both expressions approach the form 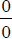, the
expression 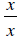will approach 1 in the limit and
the
expression 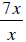will have a limiting value of 7.
Thus, limits which approach the form 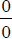must be
evaluated by alternative means since this expression does not determine a unique
limit.
The Zero Discriminant and the Zero Determinant
The discriminant is a very useful tool in Algebra. The descriminant of the
quadratic
polynomial, ax2 + bx + c , is the expression b2 − 4ac,
where values a, b, and c come from the
polynomial. The descriminant allows the students to determine how many solutions
there are to
a quadratic polynomial before plugging the coefficients into the quadratic
formula. The graph of
a quadratic polynomial is a parabola, and the discriminant can be used to
determine the number
of x- intercepts of the parabola . Specifically, if the discriminant is equal to a
negative number,
the parabola does not cross the x-axis; if the discriminant is equal to 0, then
the parabola has one
x-intercept (i.e. the vertex of the parabola is on the x-axis); if the
discriminant is positive, then
the parabola has two, distinct x-intercepts.
It is interesting to show that shifting a parabola horizontally does not change
the
discriminant. To do this, we can compare the equation y = x2 + 0 (a
parabola that opens
upwards and has its vertex at the origin) with the equation y = (x − 3)2
+ 0 (a parabola that opens
upwards with vertex (3,0); a horizontal shift of the first equation ).
Evaluating the descrimiant of
the first parabola results in 02 − 4(1)(0) , which is equal to zero.
The second equation can be
written as y = x2 − 6x + 9, which has determinant (−6)2 −
4(1)(9)=36−36 = 0. Similarly, any
horizontal shift of the equation y = x2 + 0 results in a zero
discriminant, thus the discriminant in
this example is invariant under horizontal translation. However, the
discriminant will vary under
vertical translations because the number of x-intercepts can change as the
parabola moves up or
down
The quadratic formula indicates that solutions to the quadratic equation ax2
+ bx + c = 0
are given by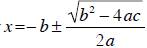
. Notice that the discriminant
appears in this formula. Again,
the discriminant plays an important role in evaluating the quadratic formula; if
the discriminant
is equal to zero, the quadratic formula reduces to x =− b ± 0 , so that x=− b is
the only solution.
A way to obtain information about two lines in the x-y coordinate plane in a
system of
equations is to set up a 2 by 2 matrix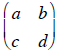 
where
the entries are the parameters in the
equations ax+ by = j and cx+ dy = k.
Solving ax + by = j and cx+ dy = k for y gives:
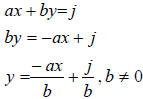and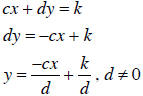 
If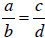 
, then the graphs of the lines determined
by these two equations have the same slope,
and so are either parallel lines or the same exact line. If we consider the
cross products of the
proportion 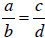, we obtain ad = bc, or ad - bc =
0. The expression ad – bc also happens to be
the determinant of the matrix
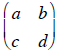. Based on the
argument above, if the determinant of a
matrix whose entries are obtained from two linear equations is equal to zero,
then the two lines
have the same slope. This means that the two lines are
parallel (if j and k are distinct) or they
are the same line (if j = k).
