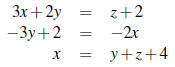Math 141 - Week in Review #2

Section 2.1 - Systems of Linear Equations

• When a system of linear equations has only two variables , each equation represents a line and “solving the system”
means finding all points the lines have in common .

• For any system of linear equations (with finitely many variables ), there are only 3 possibilities for the solution:
(1) a unique solution, (2) infinitely many solutions, or (3) no solution.

• If a system of equations has infinitely many solutions, you MUST give the parametric solution for the system .

Section 2.4 - Matrices

• The size of a matrix is always number of rows × number of columns.

• c_ij represents the entry of the matrix C in row i and column j.

• To add and subtract matrices , they must be the same size.

• When adding or subtracting matrices, add or subtract corresponding entries.

• A scalar product is computed by multiplying each entry of a matrix by a scalar (a number).

• Transpose - The rows of the matrix A become the columns of A^T .

Section 2.5 - Multiplication of Matrices

• The matrix product AB can be computed only if the number of columns of A equals the number of rows of B.

• If C = AB, then c_ij is computed by multiplying the i^th row of A by the j^th column of B.

• Identity Matrix - Denoted by I_n, the identity matrix is the n×n matrix with 1’s down the main diagonal (from upper
left corner to lower right corner) and 0’s for all other entries.

• If A is m×n, then AI_n = A and I_mA = A.

Section 2.6 - The Inverse of a Square Matrix

• Only square matrices can have inverses, but not all square matrices have inverses.

• A square matrix that does not have an inverse is called a singular matrix.

• The inverse of A, denoted A^-1, is the square n×n matrix such that AA^-1 = A^-1A = I_n.

• Systems of equations can be represented as a matrix equation of the form AX = B where A is the coefficient matrix ,
X is a column vector containing the variables, and B is a column vector containing constants.

• If A has an inverse, the solution to the matrix equation is X = A^-1B.

• If A does not have an inverse (i.e., if A is singular), this does NOT imply the system has no solution. It simply
means that you must use another method to solve the system .

1. Solve the system of equations

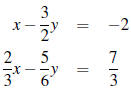
2. Solve the system of equations

3x−6y = 18

−2x+4y = −12

3. (a) Find the value of k so that the given system has no solution.

7x−5y = −3

3x+ky = 15

(b) Is it possible to find a value of k so that the system has infinitely many solutions? Explain.

(c) For what value(s) of k will the system have a unique solution?

For the next 3 exercises, set up the system of equations but do not solve.

4. (#49, pg. 74 of Finite Mathematics by Lial , et. al.) The U-Drive Rent-A-Truck Co. plans to spend $6 million on 200 new vehicles. Each
van will cost $20,000, each small truck $30,000, and each large truck $50,000. Past experience shows that they
need twice as many vans as small trucks. How many of each kind of vehicle can they buy?

5. A cashier has a total of 96 bills in his register in one-, five-, and ten-dollar denominations. If he has three times as
many fives as ones, and if the number of ones and fives combined is half of the number of tens he has, how many
bills of each denomination does he have in his register?

6. Random, Inc. makes picture collates in three sizes. A small collage requires 30 minutes of cutting time and 36
minutes of pasting time. A medium collage requires 60 minutes of cutting time and 54 minutes for pasting. A
large collage requires 90 minutes for cutting and 72 minutes for pasting. There are 380 labor hours available for
cutting and 330 labor hours available for pasting each week. If the company wants to run at full capacity, how
many collages of each size should be made each week?

7. Let 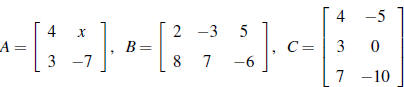, and 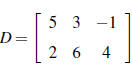. Compute each of the

following:

(a) B+3D

(b) 2C+B

(c) 4D−3C^T



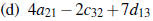
(e) DB

(f) BC

(g) CD^T

(h) BB^T

(i) A²

8. Solve for x and y:

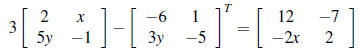
9. The times (in minutes) required for assembling, testing, and packaging large and small capacity food processors
are shown in the following table:

(a) Define a matrix T that summarizes the above data.

(b) Let M =[100 200]represent the number of large and small food processors ordered , respectively. Find
MT and explain the meaning of its entries.

(c) If assembling costs $3 per minute, testing costs $1 per minute, and packaging costs $2 per minute, find a
matrix C that, when multiplied with T, gives the total cost for making each size of food processor.

10. If 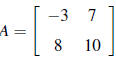find A^-1.

11. If 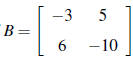, find B^-1.

12. Solve the following system of equations using matrix inverses.