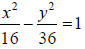Math 185 - Supplement

Chapter 6 – Section 1: Graphing Parabolas

When graphing a parabola, follow the following steps :

A. Find the vertex, focus, directrix, and the direction of the parabola.

B. Find the endpoints of the focal chord by adding and subtracting 2c to either the x-value or the y-
value of the focus depending on the direction of the parabola.

C. Plot and label the vertex, focus, and the endpoints of the focal chord in point form, draw the curve of
the parabola with a solid line , draw the directrix with a dashed line, and label the directrix with its
equation.

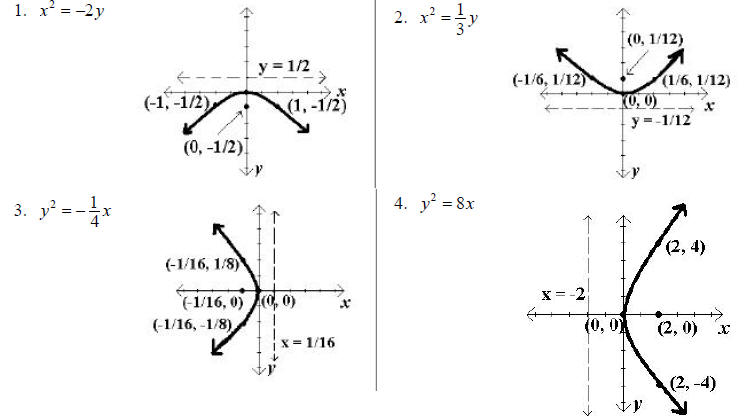
Example: Graph

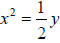
A. The vertex is (0, 0) and the standard form is x² = 4cy. Therefore,1/2=4c and .c =1/8 Because x is the
squared term and c is positive, the parabola opens up. The focus must therefore be on the y-axis
above (0, 0). Since c=1/8 the focus must be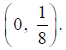Since the parabola opens up, the directrix must
be parallel to the x-axis and below (0, 0). Therefore the equation of the directrix is y = -1/8

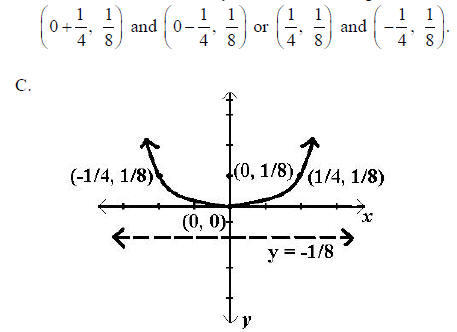
B. If c = 1/8 then 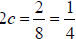 Since the parabola opens up,1/4 is added and subtracted from the x value
of the focus while the y value is unchanged. Therefore, the endpoints of the focal chord are

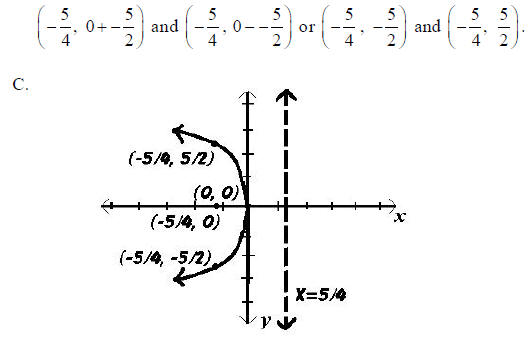
Example: Graph y² = -5x

A. The vertex is (0, 0), and the standard form is y² = 4cx. Therefore, -5 = 4c and . c = -5/4
Because y is the squared term and c is negative , the parabola opens left. The focus must therefore be on the x-axis
left of (0, 0). Since c =-5/4 the focus must be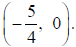Since the parabola opens left, the directrix
must be parallel to the y-axis and right of (0, 0). Therefore the equation of the directrix is x = 5/4

B. If c =-5/4 then 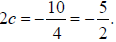Since the parabola opens left, -5/2 is added and subtracted from the y
value of the focus while the x value is unchanged. Therefore, the endpoints of the focal chord are

Exercises for Graphing Parabolas

Graph the following parabolas. Label the vertex, focus, and endpoints of the focal chord. Draw the directrix
and label with its equation.

Chapter 6 – Section 1: Additional Application Problems

5. Translate into a mathematical model and solve:
The diameter of a parabolic flashlight is 4 centimeters. The focal length (distance from the focus to the
parabolic surface) is 0.5 centimeters. Determine the maximum depth of the flashlight. Round the answer
to the nearest centimeter. Include correct units.

a. Equation of parabola:_____________________

b. Depth:_____________

6. Translate into a mathematical model and solve:
A parabolic satellite TV receiving dish will have a receiver placed at the focus. Where should the
receiver be placed if the dish is 3 feet in diameter and has a depth of 1 foot? Round the answer to 2
decimal places .

a. Equation of parabola:___________________

b. The receiver should be placed ____ feet from the vertex.

Chapter 6, Section 2 – Additional Application Problem

7. Translate into a mathematical model and solve:

An arch of a bridge has the shape of the top half of an ellipse . The arch is 40 feet wide and 12 feet high
at the center. Find the equation of the complete ellipse. Find the height of the arch 10 feet from the
center at the bottom. Round to the nearest hundredth.

a. Equation of ellipse: ____________________
b. Height of arch:________________________ Include correct units.

Chapter 6, Section 2 – Finding the Equation of a Hyperbola given vertices and asymptotes

Find the equation of the hyperbola with vertices (6, 0) and (–6, 0) and asymptotes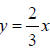 and.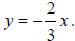

Solution :

Since the vertices are (±6,0) , the x-axis must be the major axis, the center must be (0, 0), the general
equation to be used must be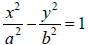 , and a must be 6. Therefore, the equation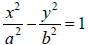 can be written
with confidence. Only b still needs to be found. The slope of the equation for the asymptote of a hyperbola
is the change in y divided by the change in x. 6 is the change in x and b is the change in y, so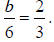
Solving this proportion gives b = 4 , and the equation of the hyperbola is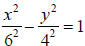 or

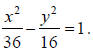
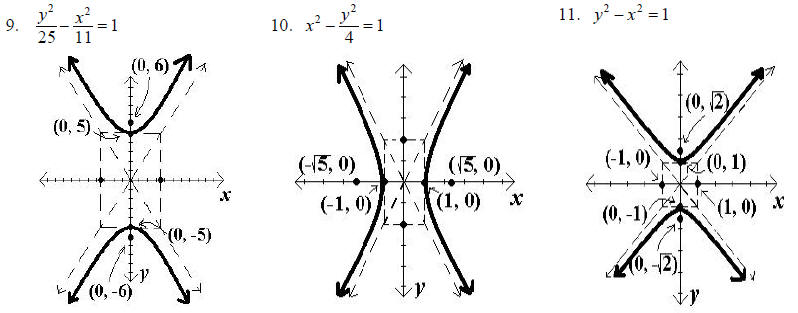
Chapter 6, Section 2 – Additional Exercise for Finding Hyperbola Equations

8. Find the equation of the hyperbola with vertices (–4, 0) and (4, 0) and asymptotes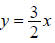and

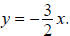
Chapter 6, Section 2 – Graphing Hyperbolas

When graphing a hyperbola, follow the following steps:

A. Determine the major axis, the center, and the vertices. Plot and label the vertices.
B. Determine helpful points on the other axis and use these points and the vertices to draw a box around
the center of the hyperbola.
C. Draw the asymptotes through the corners of the box using dashed lines.
D. Find the foci by using c² =a² +b² to find c. Add and subtract c to either the x or the y value of the
center of the hyperbola depending on the direction the hyperbola opens.

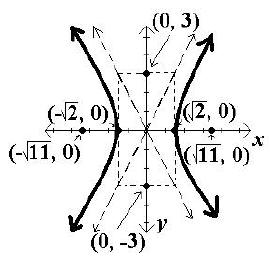
Example: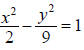

A. Because the x² is positive, the major axis is the x-axis, the
standard form of the equation is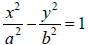 , and the
center is (0, 0). Since 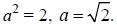Since the major axis
is the x-axis, the vertices are found by adding and
subtracting a to the x value of the center giving
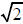( , 0) and (- 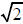, 0).

Plot and label the vertices.

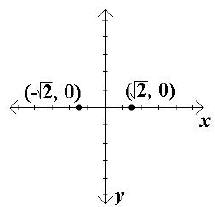
B. Helpful points on the y-axis are found by adding and
subtracting b to the y value of the center. Since b² = 9,
b = 3, and the helpful points are (0, 3) and (0, –3).

Plot the helpful points and draw a box around the center
using the vertices and these points. These helpful points
do not have to be labeled but certainly can be.

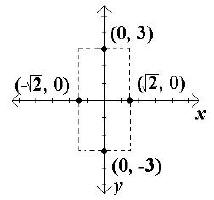
C. Draw the asymptotes through the corners of the box using
dashed lines.

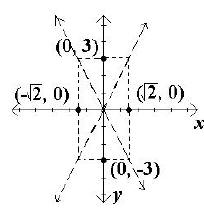
D. Since c² = a² + b² , c² = 2 + 9 = 11, and c = 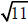. Because
the major axis is the x-axis, c is added and subtracted to
the x value of the center. Therefore the foci are ( 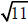, 0)
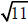and (- , 0).

Plot and label the foci. Then draw in the hyperbola
making sure that it approaches the asymptotes but does
not touch the asymptotes or look as if it will cross the
asymptote.

Example:

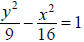
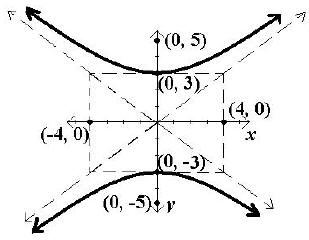
A. Because the y² is positive, the major axis is the y-axis, the standard form of the equation is
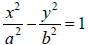, and the center is (0, 0). Since a² = 9, a = 3. Since the major axis is the y-axis, the
vertices are found by adding and subtracting a to the y value of the center giving (0, 3) and (0, –3).
Plot and label the vertices.

B. Helpful points on the x-axis are found by adding and subtracting b to the x value of the center. Since
b² = 16, b = 4, and the helpful points are (4, 0) and (–4, 0).

Plot the helpful points and draw a box around the center using the vertices and these points. These
helpful points do not have to be labeled on the graph but certainly can be.

C. Draw the asymptotes through the corners of the box using dashed lines.

D. Since c² = a² + b² , c² = 9 +16 = 25, and c = 5. Because
the major axis is the y-axis, c is added and subtracted to
the y value of the center. Therefore the foci are (0, 5)
and (0, –5).

Plot and label the foci. Then draw in the hyperbola
making sure that it approaches the asymptotes but does
not touch the asymptotes or look as if it will cross the
asymptote.

Chapter 6, Section 2 – Exercises for Graphing Hyperbolas

Graph each of the following. Label the vertices, and the foci. Graph must approach directly drawn
asymptotes, if applicable.

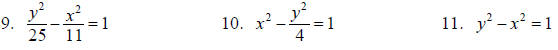
Answers for Chapter 6, Section 1 & 2 Exercises

5. a. Equation: x² = 2 y or y² = 2x; either is correct  b. 2 centimeters
6. a. Equation: 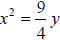or ;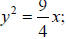 either is correct. b. 0.56

7. a. Equation: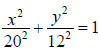or 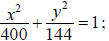 either is correct.  b. 10.39 feet

8.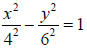or