Linear Algebra

Read for Monday section 1.6 which goes into
the solutions of linear systems of equations in a
little more detail than we already have.

Due Monday. Exercises from section 1.4: 11-13,
19, T.10, T.24, and T.30.

Due next Friday. Exercises from section 1.5: 1-
2, 5-6, 15-17.

Last time. We looked at more properties of the
matrix operations , powers of matrices, symmetric
and skew symmetric matrices.

Quiz Today. Covering through section 1.3.
Today. Finish discussion started on Wednesday.
If we have time, we'll begin a discussion on the
important concept of linear transformations , also
called matrix transformations, in section 1.5.

Matrix transformations. One of the most im-
portant uses of matrices is for describing linear
transformations of the plane R², of space R³, and
of higher dimensional spaces Rⁿ. Before getting
to the general definition of linear transformations,
we'll look at a few in the plane and space.

Geometric vectors. We'll represent an n-vector
as a straight arrow in Rⁿ. Today, we'll always take
one end of the vector, the tail, to be the origin

(0, 0,... , 0). Then, the head of the vector

is the point in Rⁿ. For example,
we'll draw the vector 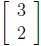as an arrow that starts
at the origin (0, 0) in the plane R² and ends at the
point (3, 2). This way we identify a column vector
with an ordered pair , so we're treating vectors as
points.

Square 2 × 2 matrices describe linear trans-
formations of the plane. For example, consider
the 2 × 2 matrix

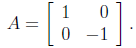
Now, take a generic point (x, y) in the plane, but
treat it as the vector 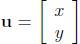. We can form the
matrix product Au, since the number of rows of A
equals the number of columns of u, to get another
vector v = Au.

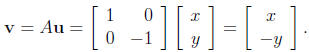
Thus, the matrix A transforms the point (x, y) to
the point f(x, y) = (x,-y). You'll recognize this
right away as a reflection across the x-axis.

Every 2 × 2 matrix describes some kind of geo-
metric transformation of the plane. But since the
origin (0, 0) is always sent to itself, not every ge-
ometric transformation can be described by a ma-
trix in this way. Only the ones that we'll call lin-
ear transformations can be described by a matrix.
There are a few others we'll look at.

Rotations. The matrix

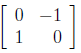
determines the transformation that sends the vec-
tor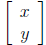to the vector 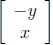. In particular, the
two "basis" vectors 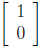and 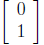are sent to the
vectors 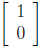and 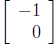, respectively. Note that
the first column of the 2 × 2 matrix says where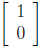
goes while the second column says where .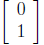

You'll recognize this transformation as a rotation
around the origin by 90°. (Our convention is to
always take counterclockwise rotations to be by a
positive number of degrees, but clockwise ones by
a negative number of degrees.)

Rotations by other angles θ can be described with
the help of trig functions . The matrix

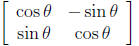
describes a rotation of the plane by an angle of θ.

For example, the matrix that describes a rotation
of the plane around the origin of 10°counterclock-
wise is

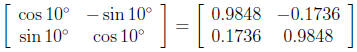
since sin 10° = 0:1736 and cos 10° = 0:9848.

All rotations preserve distance . That means that
the distance between any two vectors u and v is the
same as the distance between their images Au and
Av. Such transformations are called rigid transfor-
mations or isometries.

Reflections. We've already seen that the matrix
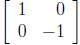describes a reflection across the x-axis.
Likewise, 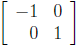describes a reflection across
the y-axis. There's a 2 × 2 matrix for reflection
across any line through the origin. What matrix
describes a reflection across the line y = x?

Note that reflections, like rotations , are trans-
formations that preserve distance, that is, they're
isometries, too.

Contractions and expansions. Not all linear
transformations preserve distance. For instance,
contractions and expansions don't. The matrix
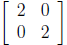sends a vector to the vector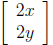
Thus, every point is sent twice as far away from the
origin. That's an expansion by a factor of 2. Ev-
ery scalar matrix where the scalar is greater than 1
describes an expansion.

When the scalar is between 0 and 1, then
t he matrix describes a contraction. For instance
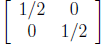moves points toward the origin half
as far away as where they started.

The particular scalar matrix 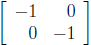sends
a point to the other side of the origin, but the same
distance away from the origin. That's the same as
a 180° rotation. These are sometimes called half
turns or point inversions.

Other scalar matrices with negative scalars de-
scribe transformations that can be thought of as
compositions of point inversions and either expan-
sions or contractions.

Sometimes the term "dilatation" is used for any
of these transformations determined by scalar ma-
trices.

Other transformations. Not every linear trans-
formation of the plane belongs to one of the classes
described above. For example, the matrix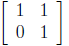

describes a "shear transformation" that fixes the

x-axis, moves points in the upper half-plane to the
right, but moves points in the lower half -plane to
the left.

Another interesting transformation is described
by the matrix 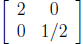Which sends the vector
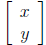to the vector 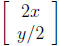The plane is trans-
formed by stretching horizontally by a factor of 2
at the same time as it's squeezed vertically.

These last two examples are plane transforma-
tions that preserve areas of figures, but don't pre-
serve distance.

If you randomly choose a two by two matrix,
it probably describes a linear transformation that
doesn't preserve distance and doesn't preserve area.

Transformation of R³. A 3 × 3 matrix describes
a transformation of space. There are many kinds
of such transformations, some isometries, some
not. Some isometries are (1) reflections across
planes that pass through the origin and (2) rota-
tions around lines that pass through the origin, but
there are others. Some transformations that aren't
isometries include dilations, contractions, shears,
but there are many others.
Linear transformation

Linear transformations between spaces. An
m by n rectangular matrix describes a linear trans-
formation from Rⁿ to R^m. We'll use the notation
Rⁿ → R^m to indicate that Rⁿ is the domain of the
transformation and R^m is the range or codomain of
the transformation.

Here, for instance, is a 2 × 3 matrix that describes
a linear transformation R³ → R²: 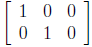It
sends the vector 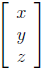in the domain R³ to the
vecto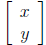r in the codomain R². This particular
transformation is a "projection" from 3-space onto
the xy-plane that forgets the z- coordinate .

A linear transformation Rⁿ → R is described

by a row matrix. For example, the matrix
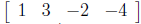describes the linear transforma-
tion R⁴ → R which sends the point (w, x, y, z) to
w + 3x - 2y - 4z.

Later in the course we'll define a linear trans-
formation L : Rⁿ → R^m to be a function that
preserves addition of vectors

L(u + v) = L(u) + L(v)

and multiplication by scalars

L(cu) = cL(u).

We'll see then that every linear transformation L :
Rⁿ → R^m can be represented by a unique m × n
matrix A, that is, L(u) = Au for each vector u ∈
Rⁿ.