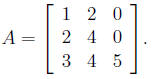ON THE FRONT OF YOUR BLUEBOOK write: (1) your name, (2) your student
ID number , (3)
your lecture section, (4) your instructor’s name and (5) a grading table. You
have 90 minutes to
work all 5 problems on the exam. Each problem is worth 20 points. Show ALL of
your work in the
bluebook and box in final answers. Start each problem on a new page. A
correct answer with no
relevant work may receive no credit, while an incorrect answer accompanied by
some correct work
may receive partial credit. Text books, class notes and calculators are NOT
permitted . One letter
size (8.5" × 11") crib sheet with anything hand written on both sides is
allowed.
1. a) Given the matrices
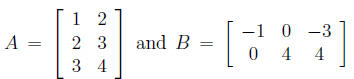
which
of the following matrix operations are defined and which are not defined? (You
do not need to give reasons or evaluate those that are defined.)
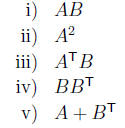
b) Determine all values of a and b for which the matrix
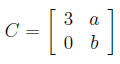
has
only one eigenvector.
c) Give an example of three 2 × 2 matrices D, E and F, with E ≠ F but DE =
DF.
d) Prove there does not exist a matrix G, with
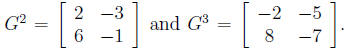
(hint:
think determinants)
2. Consider the matrix,
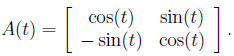
a) Compute the determinant of A(t).
b) Use your answer from part (a) to answer the following. Give reasons.
i) Are cos(t) and sin(t) linearly independent functions?
ii) Are there any values of t for which the columns of A(t) do not span R^2?
c) Compute the eigenvalues of A(t).
d) Compute the eigenvectors of A( π/2 ).
3. In this problem you will determine the equation of a parabola that passes
through the points
i) x = −1, y = 5,
ii) x = 1, y = 0,
iii) x = 3, y = 3,
as shown in the figure. Assume that the equation of the parabola is y = ax^2
+ bx + c where a, b and c are unknown coefficients.
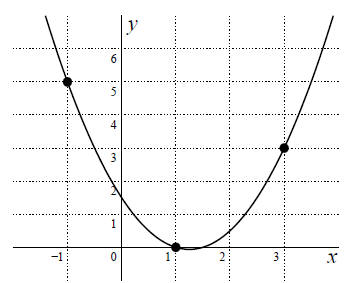
a) Substitute each (x, y) point into (1) to obtain 3 algebraic
equations that relate the 3
unknowns a , b and c.
b) Rewrite the 3 algebraic equations determined in (a) as a single
augmented matrix and
row reduce this matrix to RREF (reduced row echelon form).
c) Using your answer from (b) determine the values of a , b and c and
write the equation of the parabola .
4. Let V be a vector space and W a subset of V .
a) State the 2 closure properties that W must satisfy to be a linear
subspace.
b) Let M2,2 denote the vector space of all 2 × 2 matrices.
Let C([0, 1]) denote the vector space of all continuous functions on the
interval [0, 1].
Are the following linear subspaces ? If yes, simply write “YES” (no justification
required).
If no, write “NO” and provide reasoning.
i) W1 = {A ∈ M2,2 | A is a diagonal matrix}
ii) W2 = {A ∈ M2,2 | det(A) = 0}
iii) W3 = {f ∈ C([0, 1]) | f(0) = 1}
5. Determine all eigenvalues and eigenvectors of