Equivalent Expressions : are algebraic
expressions that have the same value no matter
what value(s) is substituted for the variable (s).
Students have various ways to check for
equivalence: using graphs and tables, or using
Properties of Real numbers. See below.Note:
Students often confuse “expression” and
“equation.” “3x” is an expression. It can be
evaluated for various values of x. However, “y
= 3x” or “12 = 3x” are equations. These two
equations have solutions . In the case of y = 3x
there are an infinite number of solutions: (1, 3),
(2, 6) etc. In the case of 12 = 3x there is only
one solution, x = 4. Likewise: 2x2 + 10x is an
expression which can be evaluated: while 2x2 +
10x = 12 is an equation which can be solved .
|
1. Write 2 expressions for the number of
1-footsquare
tiles, N, needed to make a border
around a square pool with sides of length s feet.
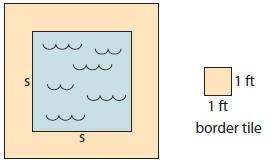
The expression for N depends on how a student
visualizes the area of the tiled border. A
student might say that the border is made of 4
strips, each s tiles long, and 4 corners, as
below.
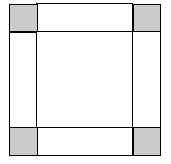
In this case the student will say that the number
of tiles needed is N = 4s + 4.Or the student might see this as 4 strips, each
(s + 1) tiles long, as below.
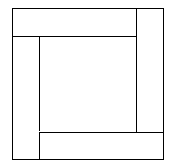
In this case the student will say that
N = 4(s+ 1) tiles are needed.
2. Determine that the two expressions for N in
example 1 are equivalent.
Students already know the meaning of
“equivalent” in terms of functions . So they could
compare the expressions “4s + 4” and “4(s + 1)”
by making a table, for various values of s.
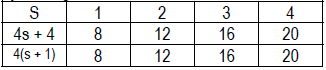
It appears that these two expressions always
have the same value, for any given value of s.
Note: Students could also use a graph to make
this comparison. However, tables and graphs
are only snapshots of SOME of the values that
an expression might take. To be sure that
these expressions are equivalent for ALL values
of the variable we need a better strategy. See
below. |
Interpret an Expression: Students who
develop familiarity with symbolic expressions
can recognize what a particular expression
might represent.Note: “3x” is a monomial because it has 1 term.
“3x + 2y” is a binomial because it has 2 terms
added. If an expression has 3 terms it is called
a trinomial. An expression with more than 3
terms is called a polynomial . (You can use
“polynomial” to refer to an expression with ANY
number of terms.) |
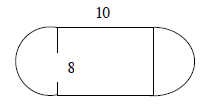
3. Sketch a pool whose area is given by
16π + 80 square feet.There are several possible answers, but
students should be able to spot a symbolic
expression related to a circle within the given
binomial expression. The term“16π” is the
area of a circle with radius 4 units. The other
term, “80”, could be a rectangular area. One
possible pool would be
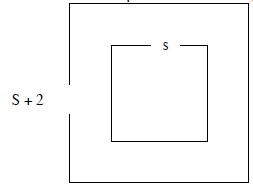
4. If a student gives the number of tiles needed
for the pool problem as N = (s + 2)2 – s2, how
did the student visualize the problem?
There are 2 squared expressions within this
polynomial: (s + 2)2 and s2. The presence of the
“square” implies a square area. “s2” is the area
of a square with sides s; “(s + 2)2” is the area of
a square with side (s + 2). On the sketch of the
original pool the student could have visualized
this as the outer square – the inner square.
 |
| Properties of Real Numbers
The Commutative Property: of addition
states that the order of addition of real numbers
does not matter. a + b = b + a for all real values
of a and b.
Note: Multiplication of real numbers also has
this property. Subtraction and division of real
numbers do not have this property. For
example, 8 – 3 is not the same as 3 – 8.
The Associative Property: of addition of real
numbers states that when adding 3 (or more)
real numbers you may group them in pairs and
add, using any groupings.
a + b + c = (a + b) + c = a + (b + c).
Note: Multiplication of real numbers also has
this property, but subtraction and division do
not. For example,
12 ÷ 4 ÷ 2 = (12 ÷ 4) ÷ 2 = 3 ÷ 2 = 1.5.
12 ÷ 4 ÷ 2 ≠ 12 ÷ (4 ÷ 2) = 12 ÷ 2 = 6.
There is a particular order of operations that we
use when we have several operations to do to
evaluate an expression. In this case we do the
divisions in order from the left. As we have
seen, if there are only additions of
multiplications in the expression then we can
change the order, or group them in any way.
See Accentuate the Negative for more on Order
of Operations.
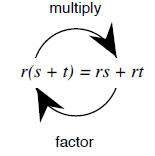
Distributive Property :
• If an expression is written as a factor
multiplied by a sum of two are more
terms, the distributive property can be
applied to multiply or expand the
factor by each term in the sum.
• If an expression is written as a sum of
terms and the terms have a common
factor, the distributive property can be
applied to rewrite the expression as the
common factor multiplied by a sum of
two or more terms. This process is
called factoring.
Note: The distributive property was first
introduced in Accentuate the Negative and
extended in Frogs, Fleas, and Painted Cubes ,
to include two binomials, (a + b)(c + d). |
5. Show that 4s + 4, 4(s + 1) and 2(s + 2) + 2s
are equivalent by using properties of real
numbers.4(s + 1) = 4s + 4
(using the Distributive
property to multiply each of
the terms of “s + 1” by 4.)
2(s + 2) + 2s = 2s + 4 + 2s (using the
Distributive
Property to multiply
each
of the terms of
“s + 2” by 2)
= 2s + 2s + 4 (Using the
Commutative
Property of
addition to change
the order)
= (2s + 2s) + 4 (Using the
Associative
Property)
= 4s + 4 (Using the Distributive
Property)
Note: 2s + 2s can be written as s(2 + 2) or 4s,
using the Distributive Property to factor 2s +
2s. Textbooks often refer to terms like 2s and
2s as “like terms” because they have the
same variable component. This permits
factoring. For example, 3xy + 5xy = xy(3 + 5) =
8xy. In this example “3xy” and “5xy” are like
terms. BUT, 3x + 5xy = x(3 + 5y) ≠ 8xy,
because “3x” and “5xy” are not like terms.
6. Suppose a checking account contains $100
at the start of the week. Three checks are
written during the week, one for $x and two for
$(x + 1). Write an expression for the balance in
the account at the end of the week in two ways:
The balance in dollars is 100 – x – 2(x + 1).
This can be written as 100 – x – 2x – 2, or as
100 – 3x – 2 or as 98 – 3x, using properties of
Real numbers to rewrite this expression in
equivalent forms.
Note: the last part of the original expression is
“-2(x + 1).” We are multiplying by –2, hence the
“–2x – 2” in the expanded form.
7. Write in factored form: 5x + 15 + 10z.
Each of the terms of this trinomial have “5” as a
factor. Therefore, we can use the Distributive
Property to write this as 5(x + 3 + 2z).
8. Write in factored form: 5x + 10x2.
Each of the terms of this binomial have “5” and
“x” as factors. Therefore, using the Distributive
Property, we can rewrite this as 5x(1 + 2x). |



