Here are some answers in this color!
Math 46 class, this is what your final looks like so far.
Some of the problems will be extremely similar to
problems you’ve had on exams already!
Take-home essay question, worth 15% of grade – see web
site, we discussed this in class. Make sure that EACH
sentence contains factual support for your ideas!
(1) Problem on dividing a circle up into fractional parts.
This involves representing fractions as portions of
circles, and also involves adding fractions , and is like the Egyptian fraction
problems we went over
carefully on the last day of class.
Example: use Egyptian fractions to divide 6 pies among 7 people.
6/7=1/2 + 1/3+1/42, so everyone gets ½, 1/3, and 1/42 of a pie.
(2) Alternate multiplication methods, like Russian Peasant
method, as on the take-home exam.
Example: use Russian Peasant multiplication to multiply 255 by 312.
See the text. You might divide 312 repeatedly by 2, getting 156, 78, 39, 19, 9,
4, 2, and 1. Then you
double 255 repeatedly, getting 510, 1020, 2040, 4080, 8160, 16,320, 32,640, and
65,280. Then add the
numbers opposite the odd numbers, etc. On a problem like this, make sure you get
the correct product!!!
(3) Pigeonhole principle problem. Like the one on your
first exam, and those we went over in detail on the
last day of class.
Example: Given any seven numbers chosen from {–32, –16, –8, –4, –2, –1, 1, 2,
4, 8, 16, 32}, explain
why there will always be
(a) A pair with sum 0. Use pairs (–32,32),(–16,16),…(–1,1) as pigeonholes, etc.
(b) A pair with quotient of –1. Use pairs (–32,32),(–16,16),…(–1,1)
(c) A pair with quotient of 2. Use pairs (–32,-16),(–8,-4),(–2,–1),(1,2),
(4,8),(16,32)
(d) A pair with product of –32. Use pairs (–32,1),(–16,2), etc.
(e) A pair whose sum is evenly divisible by 5. Use same pairs as (a), or
(–32,–8),(–16,–4),(–
2,2),(–1,1),(4,16),(8,32).
(f) In each case above, can you find six numbers that don’t exhibit the
property? Pick one from
each pigeonhole.
(4) Methods for comparing two fractions , without finding a
common denominator or converting both to
decimals (which is like finding a common denominator !) Like the class activity
in which we used
“alternative” methods to make the comparisons !
Example: explain which is larger, 8/21 or 16/45.
One method: 8/21 = 16/42, which is larger since numerator is now same, but
denominator < 45.
Another: 8/21 = 1/3 + 1/21, while 16/45 = 1/3 + 1/45.
(5) Pattern problem, like that on exam 1: given a pattern
in boxes 0 through 6 or 7, extend the pattern to a
different part of the plane.
Example: see exam 1.
(6) Divisibility tests for 2,3,4,5,6,9,10, and 11. I’ll
give you a problem involving 2 or 3 of these. Note that if
m and n have no factors in common , then a number is divisible by mn only if it
passes the divisibility
tests for m and n separately. Thus in order to be divisible by 10, a number must
be divisible by both 2
and 5 (in other words, end in a 0!) So, for example, what is a divisibility test
for 15?
Example: What digit must A be in order for 23232357A5323232 to be divisible
by 9? To be divisible by
11? Is there a digit that makes the number divisible by 198? (Hint 198=2 X 99.)
If A = 7 it will be divisible by 11 and 9. Since it’s even it’s also divisible
by 9 X 11 X 2=198.
(7) Some true/false or select the correct answer problems
on the history of number systems. If you’ve read
the chapter, you’ll be able to find the answers, even if you don’t remember them
quickly, by quickly
finding your way to the answer in the book!
(8) Changing from base ten to another base or vice versa,
as in the take-home test.
Example: Rewrite 12345 in base ten. Rewrite 123410 in base six and base two.
12345 = 1(125)+2(25)+3(5)+4(1)=19410. 123410 = 54146 = 100100100102.
(9) Proportion problem like the calculations you had to do
in the Barbie activity, or a calculation involving
proportional reasoning.
Example: A six foot tall tree casts a shadow of length 42”. At the same time
a taller tree casts a shadow
of length 8½ feet. How tall is the tree, in feet and inches, to the nearest
inch?
6’ = 72”, and 8½ ‘ = 100”. Set up the proportion 72/42 = x/100, x =171.42857”
=14.285714’; also
.285714 feet = (.285714)(12) = 3.428 inches, rounding off to 14 feet, 3 inches.
(10) Venn diagram problem like the one on your first exam.
Example: see first exam.
(11) Visual and other explanations for fraction
multiplication and division.
Example: give a visual explanation for the common algorithm for multiplying
the fractions 4/9 and 5/7.
Give an explanation for how to divide 4/9 by 5/7 without using “invert and
multiply” or use of a
calculator. We did these in last class.
(12) Finding the factors, prime factorization, GCD, and
LCM of two numbers .
Example: Find the LCM and GCD of 2700 and 25,200. How many factors does 2700
have?
Find the GCD = 180 using the Euclidean Algorithm, then the LCM =
(2700)(25200)/180=37800, or
factor the numbers:
25200 = 23 • 32 • 5• 7, 2700 = 22 • 33 • 52,
GCD = lower powers = 22 • 32 • 5 =180, LCM = higher powers = 23 • 33 • 52 •
7 = 37800
(13) Expressing fractions as repeating or terminating
decimals ; expressing terminating or repeating decimals
as fractions.
Example: Express 7/13 as a repeating decimal, clearly showing the repeating
digits. Express
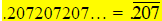as a fraction in lowest terms.
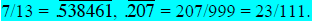
(14) Mental arithmetic techniques – be familiar with how
to apply several techniques.
Examples: see the homework under mental arithmetic.
(15) A simple cryptarithm problem, which requires a
written explanation.
Example: the “cryptarithm” problem in the take-home test, but a simpler
version.
(16) Using manipulatives to do addition and subtraction
with positive and negative integers.
Example: What calculation does the following diagram help teach?
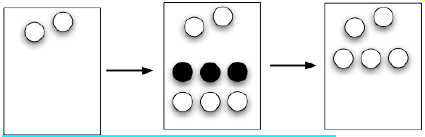
This shows either 2 – (–3) = 5, or –2 –3 = –5.
(17) Making a “Poinsot Star” by showing the multiples of a
given number on a “mod clock,” as we did when
we played names with claps and slaps.
Example: Like the review problem in the last class.
(18) An applied problem which requires converting from
fractions to percentages, and vice versa.
Examples: Non-applied problems that are similar might be “What percent does ¼
represent?” Or “40%
is what fraction of 50%; 40% is what percent of 50%? A decline from ¾ of the
population to 1/3 of the
population is a decline of what percent of the total population?”
40% is 80% of 50%. ¾ - 1/3 = 5/12 = .416 = 41.6%
(19) What are the Fibonacci numbers, how are they
constructed, how does the symbolism F1=1, F2=1, F3=2,
F4=3, F5=5, etc., work?
Example: Give the next row of the following pattern, and complete the general
formulafor the "even
case":
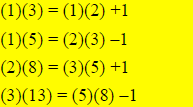
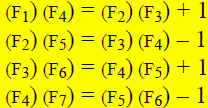
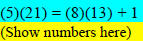
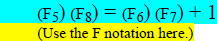
General pattern or formula when k is an even number:
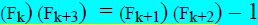
True or False. The Fibonacci numbers are found in all plant life, with no
exceptions.
True or False? Fibonacci was best known during his lifetime as the discoverer of
what are now known
as the Fibonacci numbers.
