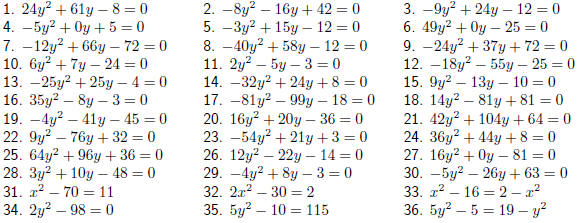22.4 Solution by the Quadratic Formula
It is not always possible to solve a quadratic equation by factorising and it is
lengthy and tedious
to solve a quadratic equations by completing the square. In these situations,
you can use the
quadratic formula that gives the solutions to any quadratic equation.
Consider the general form of the quadratic function:
f(x) = ax2 + bx + c.
Factor out the a to get :
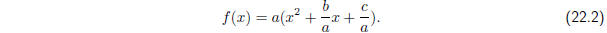
Now we need to do some detective work to figure out how to
turn (22.2) into a perfect square
plus some extra terms. We know that for a perfect square:
(m+ n)2 = m2 + 2mn + n2
and
(m− n)2 = m2 − 2mn + n2
The key is the middle term, which is 2× the first term × the second term. In
(22.2), we know
that the first term is x so 2× the second term is
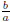 . This means that the second term is
. This means that the second term is
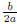 . So,
. So,
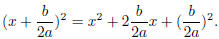
In general if you add a quantity and subtract the same
quantity, nothing has changed. This
means if we add and subtract 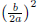 from the right
hand side of (22.2) we will get:
from the right
hand side of (22.2) we will get:
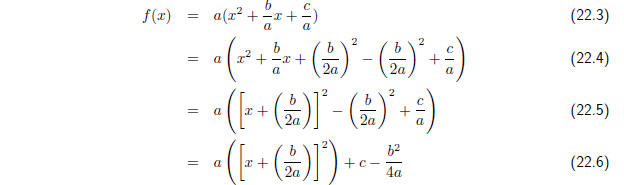
We set f(x) = 0 to find its roots, which yields:
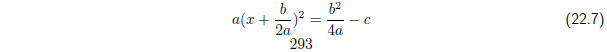
Now dividing by a and taking the square root of both sides
gives the expression
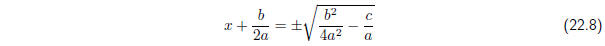
Finally, solving for x implies that
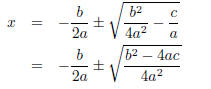
which can be further simplified to:
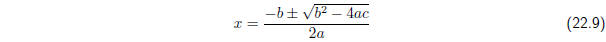
These are the solutions to the quadratic equation. Notice
that there are two solutions in general,
but these may not always exists (depending on the sign of the expression b 2 −
4ac under the
square root ). These solutions are also called the roots of the quadratic
equation.
 |
Worked Example 108: Using the quadratic formula
Question: Solve for the roots of the function f(x) = 2x2
+ 3x − 7.
Answer
Step 1 : Determine whether the equation can be factorised
The expression cannot be factorised. Therefore, the general quadratic
formula must
be used.
Step 2 : Identify the coefficients in the equation for use in the
formula
From the equation:
a = 2
b = 3
c = −7
Step 3 : Apply the quadratic formula
Always write down the formula first and then substitute the values of a ,
b and c.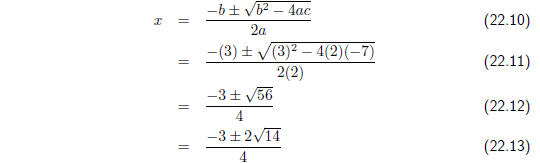
Step 4 : Write the final answer
The two roots of f (x) = 2x2 + 3x − 7 are
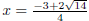 and and
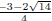 |
| |
 |
Worked Example 109: Using the
quadratic formula but no solution
Question: Solve for the solutions to the quadratic equation x2
− 5x + 8 = 0.Answer
Step 1 : Determine whether the equation can be factorised
The expression cannot be factorised. Therefore, the general quadratic
formula must
be used.
Step 2 : Identify the coefficients in the equation for use in the
formula
From the equation:
a = 1
b = −5
c = 8
Step 3 : Apply the quadratic formula
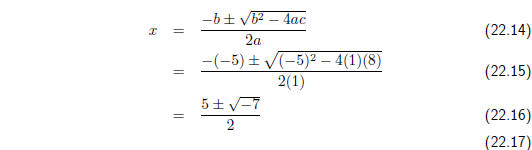
Step 4 : Write the final answer
Since the expression under the square root is negative these are not
real solutions
(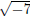 is not a real number). Therefore there are no real solutions to the
quadratic is not a real number). Therefore there are no real solutions to the
quadratic
equation x2 − 5x + 8 = 0. This means that the graph of the quadratic
function
f(x) = x2 − 5x + 8 has no x-intercepts, but that the entire graph lies
above the
x-axis. |
| |
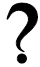 |
Exercise: Solution by the Quadratic Formula
Solve for t using the quadratic formula. |
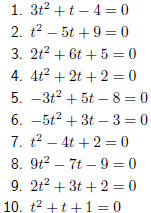
 |
Important: |
• In all the examples done so far, the solutions were left
in surd form. Answers can also
be given in decimal form , using the calculator. Read the instructions when
answering
questions in a test or exam whether to leave answers in surd form, or in decimal
form
to an appropriate number of decimal places.
• Completing the square as a method to solve a quadratic equation is only done
when
specifically asked.
 |
Exercise: Mixed Exercises
Solve the quadratic equations by either factorisation, completing the
square or
by using the quadratic formula:
• Always try to factorise first, then use the formula if the trinomial
cannot be
factorised.
• Do some of them by completing the square and then compare answers to
those
done using the other methods. |
| |