Math Problem of the Week 11

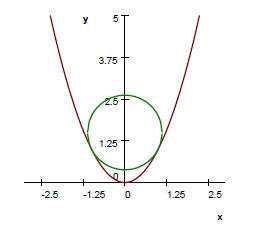
Solution by the organizers . This solution does not require the concept of curvature.
We first find the largest circle that touches the parabola at (0, 0). The center
of such disk must be located at (0, r) where r is the radius of the circle. Then the
equation of this circle is

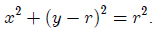
To find the largest possible r we require that this circle intersects the parabola y = x²
at a single point. Solving the system y = x² and x² + (y − r)² = r² we get

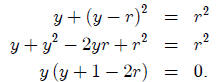
Thus we get two solution , y = 0 and y = 2r −1. However, y needs to be non- negative
since y = x², thus to have only one solution we need 2r − 1 ≤ 0. That is r ≤ 1/2.
Thus r = 1/2 is the largest radius of a circle touching the parabola at (0, 0).

Now, let 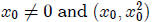be a point on the parabola . By symmetry, the largest
circle C on the concave part of the parabola touching the parabola a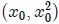t must
also touch the parabola at 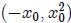, and thus have a center on the y-axis. Suppose
that the center of such circle is (0, a). The slope of the tangent line to the parabola ,
at 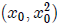, equals the derivative y' = 2x evaluated at x₀. Thus the slope of that line
is 2x₀. Since the segment joining (0, a) and 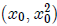is perpendicular to the tangent
line at 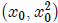, we have that

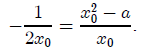
Thus 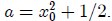. Let r be the radius of C, then we have that .
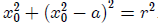Plugging the value of a we get 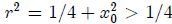. Therefore r > 1/2. Thus the
circle of radius 1/2 will freely rotate on the parabola, and 1/2 is the radius of the
largest such possible circle.
y = x²