Problem 1
Problem 2 of Homework 5 had an error. Did you notice that? I have a fix so that
you have a symmetric Hessian matrix.
Let’s do the problem again.
Compute a quadratic function f (x,y) that passes the point (2,3). At the point
(2,3), the function f (x,y) has the
gradient (1,1), the maximum curvature 3 along the direction (2,1), and the
minimum curvature 2 along the direction
(1,−2).
Now, let’s build a Hessian from curvature (not necessarily min. or max.)
requirements.
Compute a quadratic function f (x,y) that passes the point (2,3). At the point
(2,3), the function f (x,y) has the
gradient (1,1), the curvature 3 along the direction (2,1), the curvature 2 along
the direction (1,1), and the curvature 1
along the direction (3,2). Notice that these directions are not eigenvectors.
Hint: Let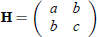 
, and solve for a ,b, and c.
Problem 2
We will compute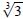 
. What is a simple function f
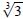(x) whose solution is ? The function f (x)
should not have
.
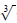Set up the Newton iteration x = g(x) for f (x). Submit f (x) and x = g(x).
Using x0 = 3 as the initial guess, perform the iteration. Submit
.
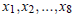Using x0 = −0.1 as the initial guess, perform the iteration. Submit
.
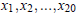Problem 3
We may start learning methods to orthonormalize a matrix. In this problem, we
will learn an iterative method.
Suppose that a matrix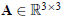 
is given, and we want to compute an orthogonal
matrix that is close to A. In fact,
the matrix closest to A in a matrix norm can be computed from the singular value
decomposition . If the SVD is
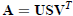, the orthogonal matrix closest to A is
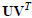. However, singular value
decomposition is expensive to
compute and complex to implement . So, let’s use the Newton’s iteration that is
simple and fast.
The idea is using A as the initial guess for the following Newton iteration,
which hopefully converge to a nearby
orthogonal matrix. Consider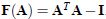 
. Its Newton iteration is
where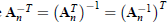 
.
Using Matlab, create a random matrix A by using the command A = (rand(3,3) -
0.5)*10;. Compute the orthogonal
matrix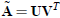 
from the singular value decomposition of A. Submit A and
,
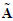which is the orthogonal matrix closest
to A in a matrix norm.
If we apply the above iteration by A = A - 1/2*inv(A’)*(A’*A - eye(3));, we will
see that A quickly converges to an
orthogonal matrix. The value of A will be fixed after a few iterations. Report
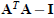per each iteration.
After A is converged, compare with ˜A. Are they same?
After A is converged, add a small random noise by using the command A = A +
(rand(3,3)-0.5)*0.1;. Then, A will
no longer be orthogonal, but will be quite close to an orthogonal matrix since
only small noise is added , and hence,
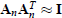and 
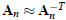. Therefore, we simplify the iteration (1) to obtain
which may converge if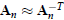 
. Notice that this iteration does not require a matrix inverse, and therefore,
much
cheaper and simpler .
Using the A (with the small noise) as the initial guess, try the iteration (2).
Does the iteration converge to an orthogonal
matrix?
Add much larger noise by the command A = A + (rand(3,3)-0.5)*10; Using (2), does
the iteration converge to an
orthogonal matrix?
