Measuring Blocks in Drafting

Team Members:
Jayson Wetherald, CTE Teacher Educator, Chambersburg MS
Joe Fullerton, Math Instructor , Lenape Technical School,
Jeff Link Auto Tech Instructor, Lenape Technical School

Title of the Lesson: Measuring Blocks in Drafting

PA Math Standard(s) Addressed by the Lesson :

2.3.8.A Develop formulas and procedures for determining measurements (e.g., time, temperature, area, length, weight, capacity, perimeter).
2.3.5.E Add and subtract measurements .
2.3.5.D Convert linear measurements within the same system.
2.9.8.D Identify, name, draw and list all properties of squares, cubes, pyramids, parallelograms, quadrilaterals, trapezoids, polygons, rectangles, rhombi, circles, spheres, triangles, prisms and cylinders.

Assessment Anchor Codes:

M8.B.1 Demonstrate an understanding of measurable attributes of objects and figures, and the units, systems and processes of measurement.
M11.B.2 Apply appropriate techniques, tools, and formulas to determine
Measurements.
M11.C.1 Analyze characteristics and properties of two - and three-dimensional
Geometric shapes and demonstrate understanding of geometric
Relationships.

1. Objective of the lesson.

Students will demonstrate a working knowledge of applying appropriate techniques, tools and formulas, to determine measurements of radius and diameter and its application in Drafting: Creating Orthographic views while recognizing it in other contexts.

2. Identify the math, math terms and vocabulary and write out the description or definitions.

*Hash marks as abbreviations for inch and feet indicators.
*Numerator = Shows how many of the original pieces we have.
*Denominator = Shows us how many pieces the original piece was cut.
*Architect Scale = A instrument used to calculate linear measurements.
* Simplified to lowest term =
*Tolerances = the acceptable accuracy of the measurement.
*Radius = the distance from the center of the circle to the outside of the circle. Half the diameter R =1/2d
*Diameter = the measurement from one side of the circle to the other side through the center of the circle. 2 times the radius D=2r

3. Note the steps, rules , underlying principles of the concept or theory and summarize.

1. The numerator represents how many sections of the inch we’ve measured.
2. The denominator represents how many sections the inch is divided into.
3. Make sure the fraction is simplified to its lowest terms.
Ex. 12/16 reduces to ¾.
4. The radius is half the diameter (R=1/2d)
5. The diameter is twice the radius (D=2r)
6. To simplify a fraction you must find the lowest common number that both the numerator and denominator divide into. In the example 12/16 both numbers are divisible by 4. When both of the numbers are divided by 4 you end up with the fraction ¾.

4. Develop 8-10 sample problems, moving from very specific Technology Education examples to more generic problems.

*Measure each line with a tolerance of +/- 16^th of an inch.
1. ____________________________
2. ___________
3. ____________________
4. _________________________
5. _______
6. What is the diameter of the wooden wheel on a toy truck that has a radius of
2-1/2”?

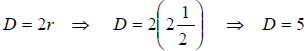
7. What is the radius of a circle that has a diameter of 2”?

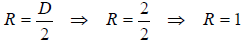
8. What measurement do we get when we add 1-3/4” and 2-15/16”?

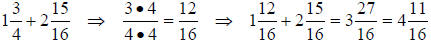
9. What fraction do we get when we add 3-1/8 and 5-1/4?

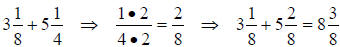
10. What fraction do we get when we multiply 3-1/4 with 6-5/16?

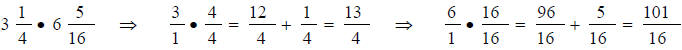
11. 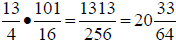  In the problem to the left you have to multiply across .

5. Document references and supplies needed to demonstrate the math concept.

*Pennsylvania Science and Technology standards
*Math Grade 8 Assessment Anchors
* Enlarged One-inch board with deviations of 1/2s, 4ths, 8ths, and 16ths
*Various sized blocks for measuring
*Worksheet to record the measurements of the blocks.
*Homework assignment measuring lines on a worksheet.

6. Describe lesson adaptations for students with special needs.

*Students will work in their table groups (peer groups) to measure each of the blocks this will allow time for the teacher to give individual guided practice.
*Extra time on task given during an activity period.

7. Provide sample handouts for students and presentation materials for teachers, as appropriate.

Title of the Lesson: Measuring Blocks

1. Introduction to the lesson.

The English system of measurement is used throughout the United States despite the use of the metric system in most other countries because of that we have to learn to use the English system of measurement and also be able to convert it. When buying any type of materials from hardware store they are for the most part in the English system of measurement. Using the English system of measurement requires the ability to use and manipulate fractions. So that we can all be on the same page with measurements we’re going to review parts of a fraction and how it applies to fractions of an inch.

2. Assess students’ math awareness by asking questions.

hat is the top number in a fraction called?
What is the bottom number in a fraction called?
What does 12/16ths simplify to?
What is Diameter?
What is Radius?

3. Demonstrate the example problem that is embedded in the automotive technology curriculum.

*What is the diameter of the wooden wheel on a toy truck that has a radius of
2-1/2”?

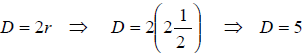
Or: Convert 2-1/2 to its decimal equivalent , which is 2.50

4. Explain the math concept or theory and show students how it applies, using the terminology of math.

*Without knowing that the diameter of a circle is twice as big as the radius of the circle we can find out vital dimensions that aren’t provided on the drawing. Draftsmen try to use as few dimensions as possible so as to not jumble up the blue print and make is hard to read.

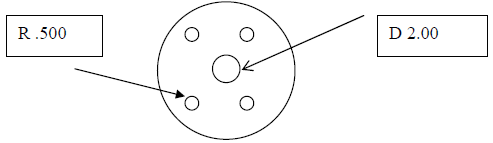
5. Demonstrate other examples as necessary.

*Using Radiuses and diameters to locate the distance between bored holes.

6. Have students explain the solutions to the problems, or demonstrate what they did to show understanding.

*Go around the classroom asking the student to determine radius and diameter. For example I would ask a student what is the radius of a circle with a diameter of 4 inches. Once the student answered move on to the next student until every student has answered.

*To complete an Orthographic drawing, students must know how to use radius and
diameter to figure out vital dimensions of a part.

7. Challenge students to write and solve their own example problems and demonstrate competency in a test situation.

Now that you understand the difference between radius and diameter here are some sample problems that you can use to create your own problems to solve.

*What is the diameter of the wooden wheel on a toy truck that has a radius of
5-3/4”?

*What is the radius of a circle that has a diameter of 9”?

*What measurement do we get when we add 1-1/2” and 5-15/16”?