MATHEMATICS CONTEST 2006 SOLUTIONS
PART I: 30 Minutes; NO CALCULATORS
Section A. Each correct answer is worth 1 point.
| 1. Evaluate: 20 + 06
Solution : a0 = 1 for any a ≠ 0, and 0b = 0 for any b ≠ 0. Therefore, 20 + 06
= 1 + 0 = 1. |
| |
| 2. The perimeter of a rectangle is 2006 inches. Its length
is 800 inches. What is its width? Solution: Perimeter equals 2L + 2W. If L = 800, 2W = 406, so W = 203 inches. |
| |
3. Express in simplest form :
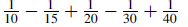 Solution: The common denominator for these fractions is 120, so
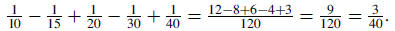 |
| |
| 4. Evaluate and write the answer in scientific notation: (280 × 106) ÷ (7 × 103)
Solution: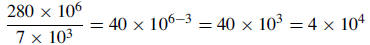 |
| |
| 5. How many of these numbers are not divisible by
9? 27, 90, 108, 792, 162, 2006, 5445 Solution: The “brute force” approach would be to divide each of
these numbers by 9, and see
which have a remainder. There is a faster approach of you know that a
number is divisible by 9
if (and only if) the sum of its digits is divisible by 9. For example,
108 is divisible by 9 because
1 + 0 + 8 = 9 is (obviously) divisible by 9. By this test, only 2006 is
not divisible by 9, so the
answer is 1. |
| |
| 6. Evaluate: 12 + 3 × 4 − 6 + 8
Solution: Follow standard order of operations: 12 + 3 × 4 − 6 + 8
= 12 + 12 − 6 + 8 = 26. |
| |
| 7. The divisor is 11, the quotient is 3, and the
remainder is 4. What is the dividend? Solution: In the equation a ÷ b = c + d/b , often written as a =
bc + d, the dividend is a, the
divisor b, the quotient c, and the remainder d. Therefore, the dividend
is a = (11)(3)+4 = 37. |
| |
| Section B. Each correct answer is worth 2 points. |
| |
8. Which one of the following expressions is not
equal to the other four?
(A) 3x(x + 2)(x − 1)  (B) −(1 −
x)(3x2 + 6x) (B) −(1 −
x)(3x2 + 6x)  (C) 3(x3 + x2 − 2) (C) 3(x3 + x2 − 2)
(D) (x + 2)(3x2 − 3x)  (E) −6x + 3x2
+ 3x3 (E) −6x + 3x2
+ 3x3Solution: C is different from the rest. This observation can be
made in a number of ways; for
example, by noting that C does not have a common factor of x (that is,
all the other expressions
equal 0 when x = 0). |
| |
9. Express as a fraction in simplest form:
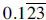 Solution 1: If 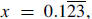 , then , then
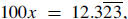 so 100x − x = 99x = 12.2. Therefore, so 100x − x = 99x = 12.2. Therefore,
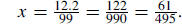
Solution 2: Note that 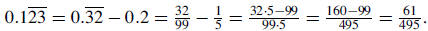 |
| |
| 10. Factor completely: ax − by − bx + ay
Solution: Group like terms:
ax − by − bx + ay = ax + ay − by − bx = a(x + y) − b(x + y) = (a − b)(x
+ y).
Equivalently ,
ax − by − bx + ay = ax − bx − by + ay = x(a − b) + y(−b + a) = (a − b)(x
+ y). |
| |
11. The degree measure of an angle of a regular
polygon cannot be
(A) 60 (B) 75 (C) 90 (D) 120 (E) 135Solution: The answer is B: The total degree measure of an n-gon
is 180(n − 2). (For example,
the angles in a triangle sum to 180°; in a
quadrilateral, they sum to 360°, etc.) Therefore,
in a
regular n-gon, an individual angle measure is
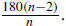 This gives 60°
when n = 6 (a regular This gives 60°
when n = 6 (a regular
hexagon), 90° for n = 4 (a square), 120◦ for n =
3 (an equilateral triangle), and 135° for n = 8
(a regular octagon). |
| |
12. Write in simplest form as an exponential
expression with a single base: 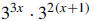
Solution: Use the rule of exponents that says
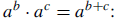
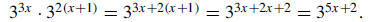 |
| |
| Section C. Each correct answer is worth 3 points. |
| |
| 13. If (x3 + 3x − 2) is divided by (x2 − 2),
what is the remainder? Solution 1: Carry out polynomial long division.
Solution 2: Any time you perform the division a ÷ b and get
quotient q and remainder r , those
four quantities are related by the equation a = b · q + r . (See the
solution to problem #7
on the previous page .) For polynomial division, the remainder r should
be a polynomial of
degree smaller than the degree of b. So we want r (a first-degree
polynomial) in the equation
x3 + 3x − 2 = (x2 − 2)q + r . In order to have an x3 term (but no x2
term) on the right side, q
must be x, so x3 + 3x − 2 = (x2 − 2)(x) + r, or r = (x3 + 3x − 2) −
(x2 − 2x) = 5x − 2. |
| |
14. Express as a single radical in simplest form:
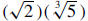 Solution: 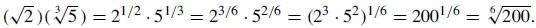 |
| |
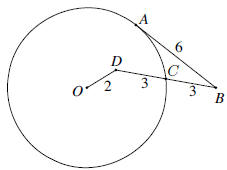
15. (See figure).
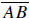 is tangent to is tangent to
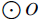 at A. If BC = 3, CD = 3, OD = 2, and AB =
6, find at A. If BC = 3, CD = 3, OD = 2, and AB =
6, find
the length of the radius of
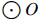 . .
Solution: Extend segment
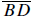 to intersect the circle at E. For any tangent
segment (like to intersect the circle at E. For any tangent
segment (like
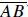 ) and ) and
secant segment (like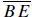 ), the lengths are related by the equation AB2 = (BC)(BE).
Therefore, ), the lengths are related by the equation AB2 = (BC)(BE).
Therefore,
BE = 12, and DE = 6.
Method 1: Extend
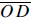 into a diameter, intersecting into a diameter, intersecting
the circle at points F and G. A formula similar to the
one used above says that for any two secants (like
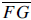
and 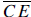 ) which intersect inside the circle, we have ) which intersect inside the circle, we have
(CD)(DE) = (FD)(DG). Therefore, (3)(6) =
(r − 2)(r + 2), so r2 = 22, and r =
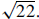 |
 |
Method 2: Let H be the midpoint of
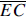 , and note that , and note that
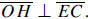 Let x = OH. Then
by the Let x = OH. Then
by the
Pythagorean theorem (applied to ∆OHD), x2 + 1.52 = 22, so x2 = 1.75. By the
Pythagorean
theorem (applied to ∆OHC), x2 + 4.52 = r2, so r2 = 22, and r =
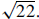
|
| |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
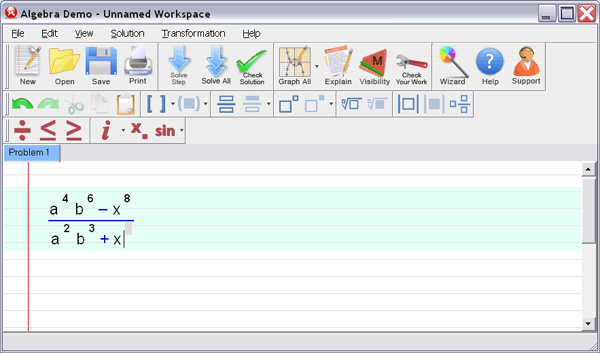
Step 2 :
Let Algebra Helper solve it:
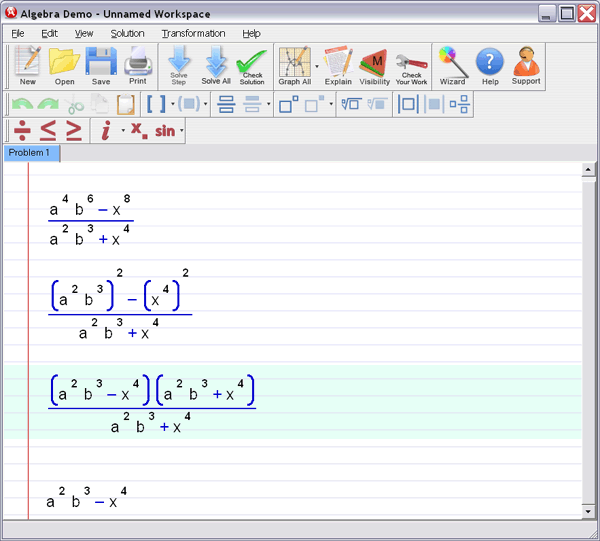
Step 3 : Ask for an explanation for the steps you don't understand:
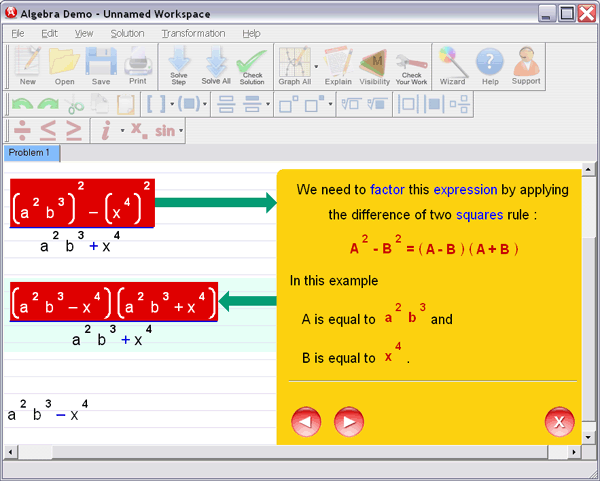
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



