A polynomial function
is a power function or
the sum of two or more
power functions, each of
which has a nonnegative
integer power. Because
polynomial functions
are built from power
functions, their domains
are all real numbers.
The graph of a polynomial
function is smooth
and unbroken. This important property of polynomial functions makes them
particularly
useful for transforming one image into another during special effects in movies,
for creating fonts for computers, and for approximating solutions to otherwise
uncomputable
problems.
Polynomials are used to morph one image into another on
Scholastic Production’s Animorphs.
In this lesson, you will explore some of the advantages of expressing
polynomials
in different equivalent forms.
INVESTIGATION 1
Need for Speed
In the previous lesson, you may have noticed that the
time needed to produce a curve on a calculator
depends upon the complexity of the equation
involved. This fact is very important to computer scientists,
mathematicians, and engineers, for whom
computation time is often a critical component of any
project. Saving computer time saves money. Super
computers such as the SGI Origin 2000 at the National
Center for Super-computing Applications at the
University of Illinois at Champaign–Urbana can cost
between 2 and 3 million dollars a year to operate .
Kray super computer
1. The form of a function rule can greatly influence
the time it takes to calculate function values or
produce its graph. In this activity, you will use your calculator to measure
computation time for polynomial functions.
a. Working in pairs, measure and record the time required to graph the function
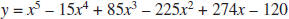
with the viewing window set to 0 ≤ x ≤ 6 and –10 ≤ y ≤ 10. One person
should watch the graph and the other should watch the time. Be sure to
turn off any other functions or plots before doing this experiment.
b. Next measure and record the time it takes to graph the function
y = (x – 1)(x – 2)(x – 3)(x – 4)(x – 5).
Be sure to turn off any other functions.
c. Verify that the function rules in Parts a and b are equivalent.
d. Which form produces the graph more quickly? What percentage of time is
saved using this form?
e. Computation time is measured in units called cycles. Suppose computing
any power, such as (1.2)4, uses twice as much computation time as does
any multiplication, subtraction, or addition , which each require 1 cycle.
How many cycles are required when
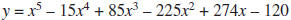
is evaluated for a particular value of x?
How many cycles are required when the equivalent rule
y = (x – 1)(x – 2)(x – 3)(x – 4)(x – 5)
is evaluated?
How does this computation time for the factored form compare to the
computation time for the standard polynomial form?
2. The factored form of a polynomial can reduce the
computation time, but
not all polynomials can be written as a product of linear factors . Another
way a polynomial can be rewritten to avoid exponents is to use nested
multiplication.
a. Verify that the polynomial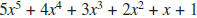 
can be rewritten
in nested form as ((((5x + 4)x + 3)x + 2)x + 1)x + 1.
b. Determine the percentage of computation time (in seconds) saved in
graphing the function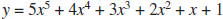 
expressed in nested
multiplication form rather than in standard polynomial form. Use the
window –2 ≤ x ≤ 2 and –40 ≤ y ≤ 40.
c. How many cycles are required to compute each form of the polynomial?
How is the cycle count related to your answer in Part b?
d. Investigate other viewing windows for the graph of the polynomial function.
Explain why this polynomial cannot be written as a product of linear
factors. Into how many linear factors can this polynomial be factored?
e. Rewrite the polynomial of Activity 1 using nested multiplication. How
does the computation time for nested multiplication compare to the computation
time for the factored form?
| Checkpoint The form of a polynomial influences computation speed as
well as the
information that can be determined by examining the form.
Write the polynomial function y = (x + 2)(x – 5)(x2 + 1) in standard
polynomial form; in nested multiplication form.
What information about the graph of a polynomial function can you get
from the factored form? From the expanded or standard form? From
the nested multiplication form?
Be prepared to discuss the importance of each form of a
polynomial with your classmates.
|
Evaluating polynomials using nested multiplication is frequently called
Horner’s Method after the English mathematician William George Horner
(1786–1837). However, evidence was published in 1911 that Paolo Ruffini
(1765–1822) had used the method 15 years before Horner. More recently, the
method has been found over 500 years before either Ruffini or Horner in the
works of Chinese mathematicians during the late Sung Dynasty: Li Chih
(1192–1279), Chu Shih-chieh (1270–1330), Ch’in Chiu-shao (c. 1202–1261)
and Yang Hui (c. 1261–1275).
On Your Own
Because evaluation of polynomial functions only requires addition, subtraction,
and multiplication, they are often used to estimate nonpolynomial functions.
Graph the function y = sin x in the window –4 ≤ x ≤ 4 and –2 ≤ y ≤ 2. Then graph
each of the following polynomial functions in the same viewing window.
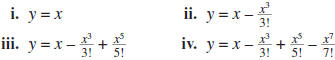
a. Compare the graphs of the polynomial functions to the
graph of the sine function.
b. Determine the zeroes of each polynomial function. How do these values compare
to the zeroes of the sine function?
c. Write the next polynomial function approximation in this sequence.
d. Compare the time it takes your calculator to graph the fourth polynomial
function
above written in standard form and in nested multiplication form.
INVESTIGATION 2
Strategic Factors
Throughout your work with quadratic and higher degree polynomial functions,
the factored form of the polynomials has played an important role. Historically,
writing polynomials in factored form was important for finding solutions to
equations.
Problems involving the solution of polynomial equations date back to the
time of the ancient Egyptians, Babylonians, and Greeks. The first systematic
presentation
of the solution of polynomial equations is attributed by some historians
to a group of Arab mathematicians starting with al-Kwarizmi (c. 800–847).
1. In her article “The Art of Algebra” (History of
Science, June 1988, pp. 129–164), Karen Parshall
describes the evolution of solving
polynomial equations.
Karen Parshall
a. She reports that a systematic solution of
the equation x2 + 10x = 39 was described
by al-Kwarizmi in the early 800s.
Describe all the methods you know for
solving this equation .
Solve this equation by reasoning with
the symbolic form itself.
b. Several centuries earlier around 250 A.D., Diophantus of Alexandria solved
the equation 630x2 + 73x = 6. Using a method of your choice, find the
solutions to this equation.
2. Until the sixteenth century, the solution of polynomial
equations involved systematic
guessing-and-testing for possible linear factors involving integers.
a. Expand the polynomial P(x) = (x – a)(x – b)(x – c), where a, b, and c are
given constants. Write the polynomial in standard form where the coefficients
of each power of x are expressions involving a, b, and c.
b. What do you observe about the constant term? How could the constant
term be used to identify possible factors of a polynomial?
c. What do you observe about the coefficient of the x 2 term?
d. How might you generalize your observations in Parts b and c so that they
apply to nth-degree polynomials? Compare your generalization with those
of other groups. Resolve any differences .
e. Use your generalization to solve the following equations.
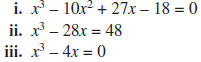
3. Rewrite each polynomial function in factored form using
information from its
graph and your generalization in Activity 2.
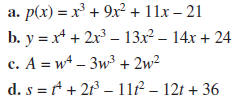
While searching for factors of a given polynomial, you
probably used a fundamental
relationship between the factors and the zeroes of the polynomial function.
Factor Theorem
The linear expression (x – b) is a factor of a polynomial function f (x)
if and
only if f (b) = 0. |
You will be asked to complete a proof of this theorem in
Organizing Task 1 (page 400).
4. The method of Activity 2 can be generalized to find factors of the form (ax –
b).
a. Without expanding completely, mentally determine the leading coefficient
and constant term of the polynomial f (x) = (–1x + 1)(3x – 2)(–5x – 4).
b. What are the zeroes of the polynomial function in Part a? How are the
zeroes related to divisors of the leading coefficient and of the constant term
of the polynomial?
c. Use your observations from Parts a and b to factor each
of the following
polynomials:
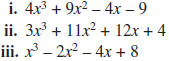
Your work in Activities 2 and 4 suggests the following
useful theorem about possible
rational zeroes of a polynomial function with integer coefficients.
Rational Zeroes Theorem
For a polynomial function with integer coefficients, if a is a divisor
of the
coefficient of the term of highest degree and b is a divisor of the
constant
term, then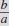 
is a possible zero of the function, with a corresponding possible
factor of the form (ax – b). |
5. You now have several ways to determine if a polynomial
of the form (x – a)
is a factor of a polynomial p(x). In this activity, you will examine a method
for finding the polynomial q(x) such that p(x) = (x – a)q(x).
a. Describe two ways of verifying that (x + 1) is a factor of
b. To find the polynomial which when multiplied by (x + 1) gives 2x3 + x2 –
4x – 3, you can use a procedure similar to long division. Polynomial division
is illustrated below. Explain how the term in bold below is chosen at
each step.
 |
|
| |
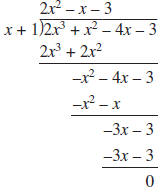| Multiply (x + 1) by 2x2 |
| Subtract |
| Multiply (x + 1) by –x |
| Subtract |
| Multiply (x + 1) by –3 |
| Subtract |
Therefore,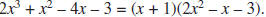 
c. Verify that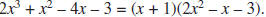
d. Show that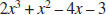 
can be written as a product of three linear
factors.
e. The polynomial x3 – 5x – 12 is equivalent to
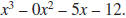
Use polynomial
division to show that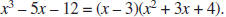 
Can x3 – 5x – 12 be written as a product of three linear factors? Explain
your reasoning.
6. Factor each polynomial into polynomials of the smallest
possible degrees.
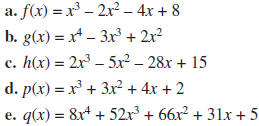
7. In Lesson 1, you discovered that the multiplicity of a
zero of a polynomial
function was related to the shape of its graph near the zero.
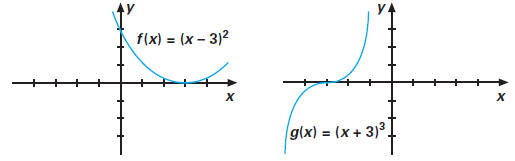
If the graph of a polynomial function touches, but does
not intersect, the x-axis
at x = a, then the zero a is repeated an even number of times . If the graph
crosses the x-axis at x = a and has a flattened appearance at this x-intercept,
then the zero a is repeated an odd number of times .
a. Compare the graphs of the polynomial functions in Activity 6 with their
factorizations. Is the expected relationship between the shape of the graph,
multiple zeroes, and repeated factors confirmed?
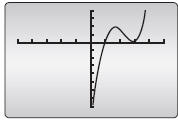
b. Find a polynomial function whose graph matches the graph shown below.
c. Use the connection between graphs, multiple zeroes, and
repeated factors
to help factor each of these polynomials into polynomials of the smallest
degrees possible.
Checkpoint
Writing and interpreting polynomials in factored form has a long history
as
a central idea in algebraic thinking .
How is the solution of a polynomial equation p(x) = 0 related to the
factored
form of the polynomial p(x)?
What strategies can you use to find the factored form of a polynomial?
How does a repeated linear factor reveal itself in the graph of a
polynomial
function?
Explain why a polynomial of degree 7 cannot have just four linear
factors
(counting the repeated factors).
Be prepared to explain your strategies for, and thinking
about, factoring polynomials to the class. |
The quadratic formula can be used to solve
second-degree polynomial equations. More complicated
formulas exist for solving third- and
fourth-degree polynomial equations. In the early
1800s, Paolo Ruffini, Neils Abel, and Evariste
Galois found ways to show that it is not possible
to solve fifth-degree equations by a formula.
Since no general formula exists for finding roots
of polynomial equations, mathematicians have
developed systematic methods for estimating
roots. One of these methods is investigated in the
MORE set.
Neils Abel
On Your Own
As you complete these tasks, think about the relationships among zeroes,
factors,
and graphs of polynomial functions.
a. Factor each polynomial into polynomials of the smallest degrees possible.
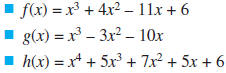
b. Sketch the graph of a fifth-degree polynomial function
that has one factor
repeated twice and a second factor repeated three times. Write a symbolic rule
that matches your graph.
c. Write an equation for the graph shown. The y- intercept is –6.
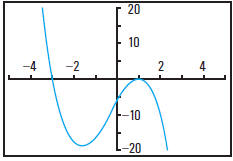
d. Andrea used the calculator graph shown at the right to
help her solve the equation
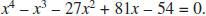She determined that the roots of the equation
were x = 1 and x = 3. Yolanda, who was
working in a group with Andrea, looked at the
graph and said there had to be another root and
found that –6 was also a solution.
Verify that 1, 3, and –6 are all roots.
How did Yolanda know there had to be another
root?
