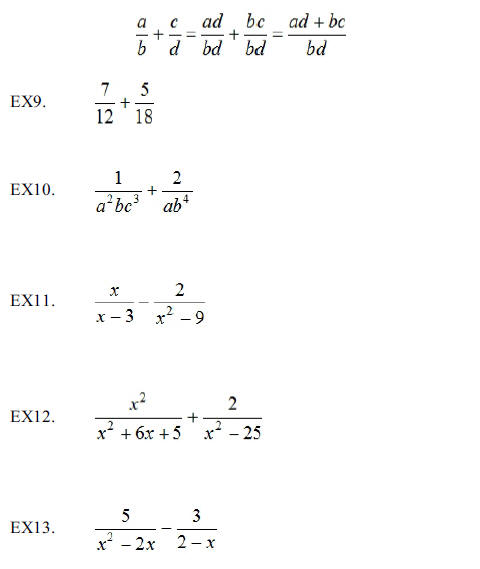Question: What does it mean to say that “a number is a
perfect square ”?
Question: Why is 9 a perfect square but 8 is not?
Question: What does it mean to say that “a variable or
term is a perfect square”?
Question: Why are the terms in the left column perfect
squares but the
terms in the right column are not perfect squares?
A geometric demonstration of the factorization of the
difference of two
perfect squares:
EX1. Factor: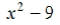
EX2. Factor: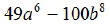
EX3. Factor: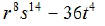
EX4. Factor: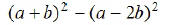
EX5. Factor: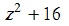
Question: What does it mean to say that “a number is a
perfect cube”?
Question: Why is 8 a perfect cube but 9 is not?
Question: What does it mean to say that “a variable or
term is a perfect
cube”?
Question: Explain why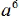 
is a perfect cube but 
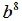is not.
Question: Find a term that is both a perfect square and a
perfect cube.
A geometric demonstration of the factorization of the
difference of two
perfect cubes.
The general form for the factorization of the difference
of two cubes :
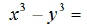
The general form for the factorization of the sum of two
cubes:
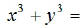
Note1. Remember that the difference (and sum) of two
perfect cubes always
factors as ______________________________________________
EX6. Factor: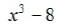
EX7. Factor: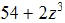
EX8. Factor: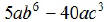
EX9. Factor: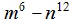
Chapter 5, Section 6: Factoring Trinomials
Note1. When factoring a polynomial, always consider the
GCF first.
Review of Factoring Techniques: Factor each of the following completely
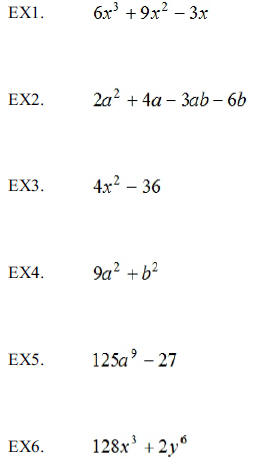
Question: What are the characteristics of a “perfect
square trinomial”?
Fill in the blank so that each of the following is a
perfect square trinomial.
Factor the resulting polynomial.
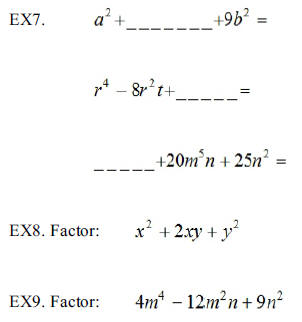
Note2. A perfect square trinomial always factors as a
__________________
___________________________________.
Note3. The square of a binomial is always a __________________________
___________________________________.
Factoring quadratic trinomials whose leading coefficient
is 1; i.e.,
polynomials of the form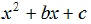 
.
Note4: To factor a quadratic trinomial of the form
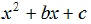, find
two integers, m and n, such that mn=c and m + n = b. If such a
pair of integers cannot be found, the trinomial is not factorable
over the integers and it is described as prime.
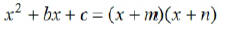
EX10. Factor: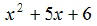
EX11. Factor: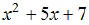
Hints for factoring quadratic trinomials of the form:
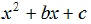
Hint #1: If c > 0, what must be true about m and n?
Hint #2: If c < 0, what must be true about m and n?
Hint #3: If c > 0 and b > 0, what must be true about m and n?
EX12. Factor: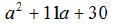
Hint #4: If c > 0 and b < 0, what must be true about m and
n?
EX13. Factor: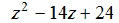 
Hint #5: If c < 0 and b > 0, what must be true about m and
n?
EX14. Factor: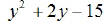
Hint #6: If c < 0 and b < 0, what must be true about m and n?
EX15. Factor: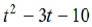 
Question: What test can be performed to determine if a
quadratic trinomial
of the form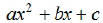 
can be factored over the
integers?
Factoring quadratic trinomials of the form
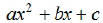using the ac or
master product method.
Step #1: Calculate the master product ac.
Step #2: Find a pair of integers m and n such that mn=c and m+n=b.
Step #3: Rewrite the original trinomial as a 4-term polynomial by
replacing bx with mx+nx.
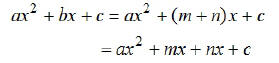
Step #4: Complete the factorization by using grouping.
EX16. Check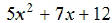 
for
factorability and factor if possible.
EX17. Check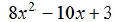 
for
factorability and factor if possible.
EX18. Check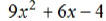 
for
factorability and factor if possible.
Chapter 5, Section 8: Solving Equations by Factoring
The ZERO FACTOR PROPERTY: If ab=0, then what must always
be true?
Def. A quadratic equation is any equation that can be
written in the form
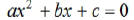where a, b, and c are real numbers and
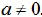
Note1. In order to solve an equation of this form by
factoring, it needs to
be written in the form given above. When it is in this form, factor
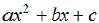and apply the Zero Product Principle. A
common
mistake that is made here is not setting the expression equal to 0 and
factoring only part of it.
EX1. Solve and check: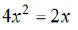 
EX2. Solve and check: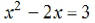 
EX3. Use the graphing calculator to solve
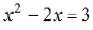
EX4. Suppose that a ball is thrown straight up into the
air with an
initial velocity of 80 fps. When will the ball hit the ground?
When will the ball be 96 feet above the ground?
Hint: Use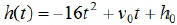 
EX5. Find a number such that the number you find is 10
less than the
square of 2 less than your number.
EX6. Find the height of the triangle shown below given
that its area is
162 square centimeters.
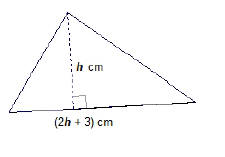
Chapter 6, Section 1: Rational Functions and
Simplifying Rational
Expressions
Question: What is a rational number?
Note1: Simplify each of the following if possible:
Def. A rational expression is
____________________________________
________________________________________________________.
Def. A rational function is ______________________________________
________________________________________________________.
Def. The domain of a rational function is ____________________________
________________________________________________________.
Def. The range of a function is ___________________________________
________________________________________________________.
EX1. Determine the domain of each of the following:
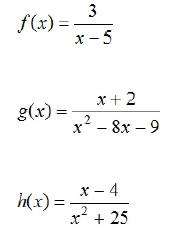
Def. A vertical asymptote is
______________________________________
_________________________________________________________
_________________________________________________________
Def. A horizontal asymptote is ___________________________________
_________________________________________________________
_________________________________________________________
EX2. Use graphing to find the domain (and range) of
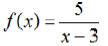
Question: What does it mean to say that “a fraction is in
simplest form”?
Note2: To simplify a fraction, factor the numerator and
the denominator
completely and divide out all the common factors. This is
equivalent to dividing the numerator and the denominator by their
GCF. This gives two numbers or terms that are relatively prime
(which means their GCF=1).
EX3. Simplify:
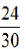
EX4. Simplify:
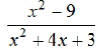
EX5. Simplify:
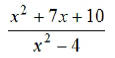
EX6. Simplify:
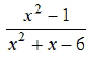
Question: How is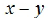 
related to 
?
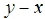EX7. Simplify:
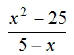
EX8. Simplify:
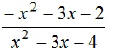
EX9. The average (mean) cost for a group to publish a
community
cookbook is given by the function
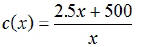
where x is the number of cookbooks printed. Find the
average
cost of the cookbooks if (a) 100 are printed (b) 300 are printed.
Chapter 6, Section 2: Multiplying and Dividing Rational
Expressions
Note1. To multiply common fractions and rational
expressions, multiply
the numerators and multiply the denominators.
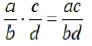
Note2. When multiplying common fractions and rational
expressions,
you may multiply and then simplify or simplify and then
multiply. The latter method is preferable when working with
rational expressions.
EX1. Find the product:
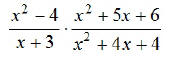
Note3. To divide common fractions and rational
expressions, multiply
BOTH the numerator and the denominator by the reciprocal of
the denominator.
EX2. Find the quotient:
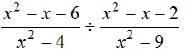
Chapter 6, Section 3: Adding and Subtracting Rational
Expressions
Note1. To add like fractions, add the numerators and put
that sum over
the common denominator.
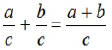
Note2. Subtraction is done in a similar manner.
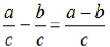
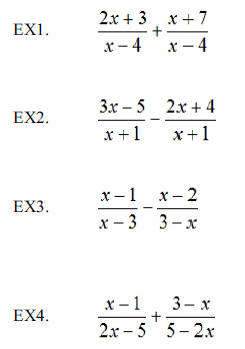
Question: What is the least common multiple (LCM) of 2
numbers?
Note3. The LCM of two numbers can be found by using prime
factorization. To find the LCM this way, prime factor each
number. The LCM will be the product of each different
prime factor raised to the highest power on that factor in any
factorization.
EX5. Use prime factorization to find the LCM of 12 and 18.
Note4. The LCM of polynomials can be found using the prime
factorization method.
EX6. Find the LCM of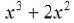 
and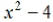 
EX7. Find the LCM of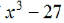 
and
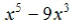
EX8. Find the LCM of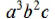 
and
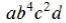[Assume a,b,c,d are prime.]
Note5. The lowest common denominator (LCD) is the LCM of
the
denominators of the fractions.
Note6. To add unlike fractions, find a common denominator
(preferably
the LCD) and then rewrite each fraction as an equivalent fraction
having as its denominator the common denominator. Add the
resulting like fractions as before.
