Matrices

Remember synthetic division ? It made polynomial division simpler by relying only on the position of the various degrees of the variable. It’s not an uncommon practice in math to let position dictate size, degree or otherwise relate to a number such as a coefficient. We do it with numbers all the time. That’s how we know that 10001 is a lot more than 101. We do exactly the same thing with linear systems . Think back to all of our Gaussian Conventions. We always said we would add or otherwise combine the columns of like variables. If we just drop out the variables, we create an array of coefficients or constants . As long as we don’t jumble the order on any row, position alone should allow us to do the various row operations . You may have already done this in the set-up for linear optimization. However, it won’t hurt to review the process.

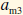
Matrix Numbering Conventions Matrices have their own peculiar vocabulary. A usual presentation of a general matrix looks like this one. We describe positions in the matrix by the row then the column. So a11 is the value in the first row and first column while would be the value in the mth row and 3rd column. The size of a matrix is the number of rows then the number of columns. If a matrix had 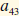as its last entry (right, lowest ), it would called a 4 by 3 matrix (abbreviated 4 ×3). The general form is described as an m× n matrix. By the way, if you wonder why Johnny can’t learn, notice that there is little consistency in whether we use the (...) or [...] to surround the matrix. Either is acceptable.

Gaussian Elimination in Matrices

Take a look at this system:

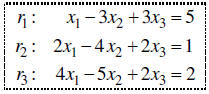
Rectangular arrangements of numbers are called matrices. (Matrix is the singular). We can create a number of
arrays from this system. Suppose we decide to just look at the coefficients. The system creates all of these
matrices:

Coefficient Matrix	Variable Matrix	Constant Matrix	Augmented Matrix

We would create the coefficient matrix related to the system. We could create the matrix of only the variables,
aptly named the variable matrix. Or, we could create the constant matrix. Each of these has use in working with
systems and the related matrix forms.

The last special form is called the augmented matrix. This is the variable matrix augmented by the constant
matrix. By the position of values we can relate back to the variable. An augmented matrix is identifiable because
we usually place a dotted vertical line where the equal sign would be. Hear’s some more good news. You
already know everything useful about working with an augmented matrix. We would transform this matrix to a
solution matrix by exactly the same conventions we used in the system.

Let’s solve this system through the augmented matrix. I choose to eliminate (zero out) the entries in the first
column below the first row.

By observation, I decided to use the linear combinations below.

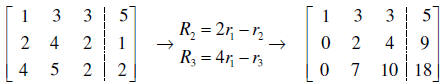
So far so good, we have a nice process going. Notice also that I did two steps at once. Since I wasn’t going to
interact rows 2 and 3, it wasn’t that hard to manipulate both at once.

Now again by observation I see that I can eliminate the 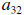entry using the linear combination below.

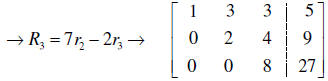
Finally, to make my life easier, I’ll scale each row to get the staircase of one’s on the diagonal.

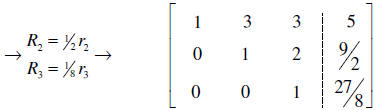
You should recognize this as the row echelon form. From here we could back- substitute to reach the solution.
However, I want to take this to the reduced row echelon form. From that form we can read the solution to the
original system. Let’s start from the bottom since it has zeros in all but the last position.

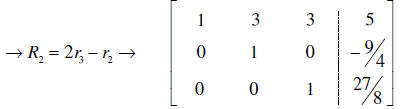
At the risk of burning out an already stressed brain, I going to zero out both 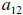and 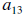. I can do this because
both elements have a 3 value. Otherwise this might take a couple of steps . Notice the linear combination uses all
three rows. Neat!

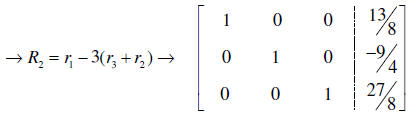
The solution is now readable as the ordered triple

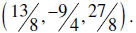
Here’s where we get into the wonderful world of answer display.

This solution can also be reflected as the column matrix to the right. (A column matrix has a
single column.) However, the appropriate way to interpret this is by realizing that it is supposed
to be juxtaposed with the variable matrix as shown.

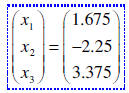
Also notice that I did revert to an exact decimal representation . The arithmetic in this problem could have been
done totally in decimal. However, had we divisors of 3, 7, 11 or other irritating denominators that create
repeating decimals, the work must be done using rational fractions . Bad things happen otherwise.