Two basic approaches to proving an implication
So far you’ve seen how to prove “if, then” statements –
assume hypothesis, prove conclusion
– and how an implication is logically equivalent to its contrapositive. This is
essentially describing not one but two methods for proving an implication.
If you prove an implication directly by assuming hypothesis, proving conclusion,
then this
is called a direct proof.
If, on the other hand, you prove an implication by proving the contrapositive,
then this
is a type of indirect proof.
You’ll no doubt have noticed, perhaps with some trepidation, the word “type” in
that
last sentence. Yes, it does mean what you suspect (and fear?!).
There is a second type of indirect proof, known as proof by contradiction or
reductio ad
absurdum.
Both indirect methods start by assuming something is false.
Suppose we want to prove p → q.
For proof by contrapositive, we prove ¬q → ¬p, so we begin by assuming q is
false.
For proof by contradiction, we begin by assuming p → q is false. We then aim to
derive
two statements which contradict one another. This contradiction will follow from
some
logical (and correct!) argument, so that the only possible error in our argument
must
come from the original step , our assumption, in which case our assumption must
have
been incorrect. The contradiction you generate will often involve a statement
you already
know is true from somewhere else or (as is more often the case) directly from
the initial
assumption.
Question: What are we really assuming when we assume p → q is
false?
Well, p → q is false in only one situation – when p is true and q is
false. So this is what
we assume at the start of every proof by contradiction.
Two Indirect Proofs
We illustrate the two methods by proving the following two statements:
(A) If x is a positive irrational number, then
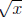is irrational.
(B) If x ≠ 0 is rational and y is irrational , then xy is irrational.
Proof of p (A) by contrapositive (you should write out what the contrapositive
is). Suppose
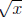is rational . Then there exist integers a, b
with b ≠ 0 such that
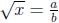. It follows that
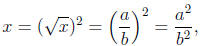
so that x is rational, as required.
Proof of (B) by contradiction. Suppose
that (B) is false.
That is, suppose there exists a rational number x ≠ 0 and irrational
number y where xy
is rational. Then there exists integers a, b, c, d, with a, b, d all non- zero ,
such that
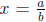
and
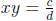. We have
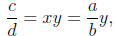
so that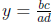 
with bc, ad integers and ad ≠
0. But this means y is rational, contradicting
our assumption that y was irrational. The only possible error in our argument is
our
original assumption, so that must have been incorrect; that is (B) must be true.
There are 3 points you should take away from these two proofs.
Firstly, in both cases we relied heavily on definitions after the initial
assumption – this is
very common .
Secondly, the contradiction generated in our proof of (B) was a contradiction on
our
original (and as it turned out, false) assumption. This might seem a problem –
but
its really ok ; the point is that in mathematics you cannot have a statement
which is
simultaneously true and false. The fact we could generate two contradictory
statements
came directly from us making a false assumption, and so there is really only one
false step
in our line of reasoning .
Thirdly, anything you prove after the initial assumption in a proof by
contradiction is
not necessarily true, but it is not necessarily false either. A proof by
contradiction only
provides you with a proof of the original statement – you cannot trust any
statement you
derive during the proof as it may be dependent on the false assumption you
started with.
