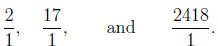Now we start talking about those things to which most
people attribute a great deal
of fear and loathing...fractions. Fractions are not really all that difficult, as
long as you
remember a few of the simple rules governing their use. So buckle your seat
belts, it might
be a bumpy ride. Once again, so we start as basic as we can get, we will begin
with the
natural numbers, and throw in 0 for good measure. So, we have
0, 1, 2, 3, …
Why do we need fractions anyway? Just as in our
development 0 and the negative numbers,
we needed them for some reason. In the previous case , we needed the negative
integers and
0 so that we would always be able to subtract. Said another way, the integers
are closed
under the operations of addition , subtraction, and multiplication. We like our
operations
to come in pairs so that when we do something we can always undo it. Subtraction
undoes
addition and vice versa. Division should undo multiplication, but right now we
can't always
do it and get an integer. We don't have an integer answer for something like
7 ÷ 2,
for instance. Thus, just as before we will throw in some
new numbers so that we are \almost"
always able to divide. These are the rational numbers , or fractions, if you
will. Now we are
ready for our first definition.
Definition 1. A fraction is a collection of symbols
of the form
a/b
where a can be any natural number or 0 and b can be any
natural number (note, not 0), and
defined to be the number so that if we multiply by b , we get a. That is,
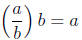
More concretely, when we write
2/3
we mean the number that if we multiply by 3 we get 2. If
we write

we mean the number that if we multiply by 317 we get 112.
You get the idea. But now
what if we write the numbers
1/2 and 2/4 ?
We think of the 1/2 as being the number if we multiply by
2, we get 1 and 2/4 as the number
we multiply by 4 and get 2. But what happens if we multiply 1/2 by 4 and
remember that we
can write 4 = (2)(2). We have
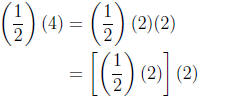 (remembering that 1
(remembering that 1
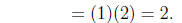
This means that we have
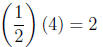
as well and that 1/2 does the same job as 2/4 . This means
that we need some way of deciding
when two fractions are going to be equal, that is when they will do the exact
same jobs.
Definition 2. For two fractions a/b and c/d , we
have
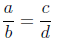 exactly when ad = bc:
exactly when ad = bc:
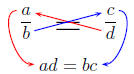
The pneumonic memory device we use to remember this is
just cross multiplying.
Example 1. Determine if the fractions are equal.
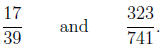
Solution . To answer this question, we simply cross
multiply.
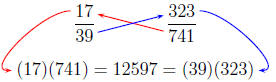
In this case, the cross multiplied terms are equal and so
the fractions are equal. }
Example 2. Determine if the fractions are equal.
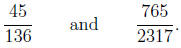
Solution. Once again, we simply cross multiply.

In this case, the cross multiplied terms are not equal so
the fractions are not equal. }
Remember that we tried to answer this question as a result
of 1/2 doing the same job
as 2/4 . The whole reason that happened was once again: : :prime factorization
of 4. The
Fundamental Theorem of Arithmetic Strikes Again! The idea is that when we
multiply a natural number by a fraction, the primes in the denominator of the
fraction
\cancel out" the primes in the natural number and the primes in the numerator
then multiply
what is \left over" after we do the canceling out. In the case of
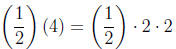
we have only one 2 to cancel out. Therefore, we are still
left with one 2 and no other primes
in the numerator so we multiply by 1 and hence
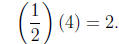
In the case of
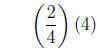
we now have two 2's in the denominator to cancel out both
2's in the 4 we are multiplying to
leave us with a 1. Therefore, in order to get the result to be a 2, we have to
throw another
2 into the numerator to compensate for canceling out both of them from the
denominator.
Let us consider another example.
Example 3. Consider what happens with the primes
when we multiply 35 by
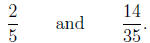
Solution. Le's look at the prime factorizations when we
multiply 2/5 by 15.
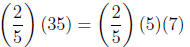
Symbolically, the 5 in the denominator and the 5 in the
numerator \cancel each other out"
and we are left with 1 in the denominator.
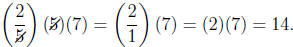
Now lets see what happens when we multiply
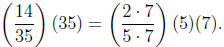
Now, since we have a 7 in the denominator, it will cancel
the 7 from the 35 we are multiplying
and we have
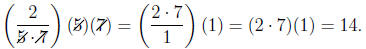
So that even though we lost a 7 by having one in the
denominator, we gained it back again
by having one in the numerator!
This example shows an important idea that also goes along
with determining when two
fractions are equal. Two fractions are equal when when the do the same job. In
order to do
the same job, if the denominator will \cancel out" more prime factors than the
other one,
then the numerator will have to put them right back. Said another way, when we
have
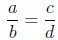
then there must be some natural number e so that
c = (a)(e) and d = (b)(e).
This means that we can rewrite
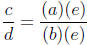
and we have the same factor in the numerator and
denominator which we can think of as
"canceling out" to give
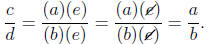
This is why we can see that
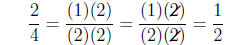
and
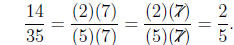
This is why when we cross multiply to see if two fractions
are equal, if we have a common
factor in the numerator and denominator that
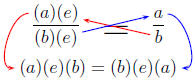
and we end up with the same primes on the left side and
the right side. By the Fundamental
Theorem of Arithmetic, there is only one way to break things down in to a
product of primes ,
and this gives us the way in which to determine if two fractions are equal,
hence \do the
same job".
Finally, remember that we did not allow the denominator of
a fraction to be 0. Once
again, when we stop and think about the \job" of a fraction the reason will
become obvious.
Suppose we did write
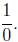
The purpose of this fraction is
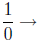 the number which when
multiplied by 0 gives you 1:
the number which when
multiplied by 0 gives you 1:
But, when we multiply 0 by anything, we get
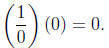
So we are multiplying something by 0 and we get 0, but we
should get 1. This makes no
sense whatsoever, so we simply don't allow the denominator to be 0. If the
denominator is
0, we say the fraction is undefined.
Now that we have said a little bit about when two
fractions will be equal, we haven't
really talked about how we will think of the natural numbers as fractions.
Definition 3. Any natural number n will be thought
of as a fraction with numerator n and
denominator 1, that is
n (as a natural number) → 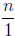 (as a rational
number):
(as a rational
number):
Therefore, for natural numbers like 2, 17, 2418, we can
think of them as the respective
fractions,