We want to look at the process of computation like a
function that takes
inputs and produces outputs; In error analysis, we are trying to analyze
what happens when we introduce small changes to either the input or output.
Errors in the input are called backward error and in the output are called
forward error.
Example 1: If our problem is to evaluate a given
function f at a particular
x, then backward error refers to changes in x, and forward error refers to
changes in f(x).
Example 2: If our problem is to find the root of a
function p, then the
backward error is the change in the function p and the forward error is the
change in the root.
It would be very nice to know how input errors (backward
error) gets
propagated through the function or algorithm into the output error (forward
error). One way to quantify this relationship is by the error magnification
factor:
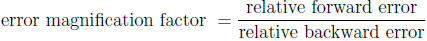
The condition number is the maximum error
magnification factor taken
over all changes in input.
Going back to our previous two examples :
Example 1A: Our problem here is to evaluate
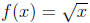at some x. Then
the relative backward error is:
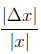
and the relative forward error is:
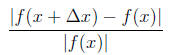
Putting these together for the error magnification factor:
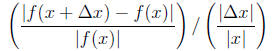
Re-writing and taking the limit as
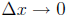, we get the condition number, k
for the function evaluation problem:
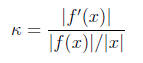
So using 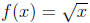we find k =
1/2. Such a small number means that
small changes in the input will generally correspond to small changes in the
output (in fact, we might expect them to be a factor of 1/2).
Example 2A: Here the problem was in root-finding.
In this case, assume
that p is a function and r is its root (p(r) = 0). Assume that
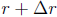is the
output of our root-finding algorithm. The backward error is
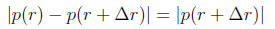
and the forward error is
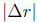
The backward error here might need some explanation: The
backward
error here is: “how do we change p so that the new function h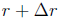as
as
its root?”. We can translate this mathematically in a number of ways- For
example, we might say that 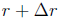is the solution
to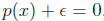 
or more
generally as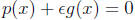 
We will use the more general form first- In that case, we
will take r to
be the exact solution to p(x) = 0 and 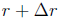to be
the exact solution to the
perturbed function,
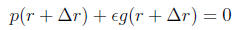
To get the error magnification, let’s see if we can relate
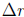to p'(r). To do
this, perform a Taylor series expansion to the equation above ,
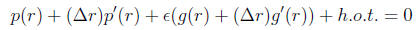
Solve for
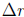and ignore the higher order terms (h.o.t.)
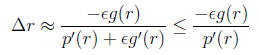
so that the error magnification factor is:
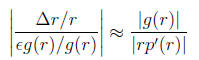
To put the previous material into numbers, suppose we are looking at the
roots to something very simple, like p(x) = x^2 − 2x + 1 = (x − 1)^2 at r = 1.
A small perturbation in the coefficients can lead to a larger change in the
roots- For example,
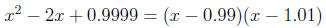
In this case, = −10-4, g(x) = 1. This led to an error of 10-2 in the roots.
In fact, the condition number of this problem is infinite since p'(r) = 0.
1.2 Multiple Roots, Part II
Consider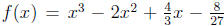 
. For future
reference, note that this
is simply the expansion of f(x) = (x − 2/3)^3. Also note that f(2/3) = 0,
f'(2/3) = 0 and f''(2/3) = 0.
In Matlab, type:
fzero(’x.^3-2*x.^2+4*x/3-8/27’,1,optimset(’Display’,’iter’))
After 64 iterations, Matlab stops with an answer where
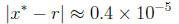
so that we only have 5 significant digits . In fact, Matlab
thinks this is the
exact solution (f(x*) is computed to be 0).
Analysis of the Error:
The problem here is that the function is too flat- In a
small interval about
x = 2/3, the IEEE arithmetic produces y− values that are all zero .
We can view the process of finding a root of a function as
equivalent to
constructing a (local) inverse and evaluating the inverse at y = 0:
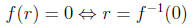
This view is made explicit in Brent’ s Method , where we
actually construct
an approximation to the inverse using a quadratic function .
1.3 The Wilkinson Polynomial
A famous polynomial with roots that are hard to find
numerically is the
Wilkinson polynomial:
W(x) = (x − 1)(x − 2)(x − 3) · · · (x − 20)
which is then expanded (an m−file with the polynomial
expanded is on our
class website, wilkpoly.m ). The problem here is that, when evaluated,
we get cancellation by subtracting nearly equal numbers (and very large)
numbers. For example,
wilkpoly(15)
ans =
-3.8085e+009
Let us consider what happens if we perturb the coefficient
of x^15. What
kind of change can we expect in the solution r = 15?
In this case,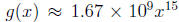 
, and
W'(15) = 5!14!, and the error
magnification factor is:
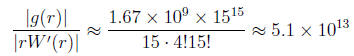
The practical implication here is that we would not be
surprised to lose 13
significant digits in computing the root.
1.3.1 Exercises:
1. Find the condition number for the problem: Evaluate the
function
f(x) = x^2 + x
2. Find the forward and backward error for the following
functions, where
r = 3/4 and the approximate root is 0.74:
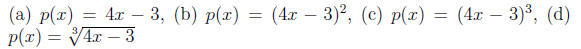
3. Let p(x) = x^2 sin(x) with r = 0.
(a) Find the multiplicity of the root r.
(b) Find the forward and backward error of the approximate root 0.01.
