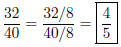Equivalent Fractions & Reducing Fractions

Table of Contents
1. Introduction
2. Equivalent Fractions
2.1. A Short Lesson
2.2. The Method
2.3. Some Quizzes
3. Reducing Fractions
Solutions to Quizzes
Section 1: Introduction 3

1. Introduction
Being able to convert one fraction into an equivalent fraction is a
very important skill that is used in adding and subtracting fractions ,
and in reducing fractions to the their lowest terms . This document
presents short tutorials on two basic skills needed in grade school:
writing equivalent fractions and reducing fractions.

2. Equivalent Fractions
Converting one fraction into an equivalent fraction is a very important
skill. This skill plays a vital role in the problem of adding or
subtracting two fractions when the denominators of the two fractions
are different.
Adding or subtracting two fractions is easy when the denominators
are the same, for example,

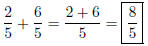
you simply add (or subtract) the numerators, as above. When the
denominators are different, such as
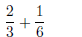(1)
the problem is not solved quite so easily.

The strategy for adding or subtracting fractions with different denominators
is to replace one or both fractions with equivalent fractions
that all have the same denominator. In the above example, it is my
idea to write the first fraction equivalent to a fraction with a denominator
of 6, that way, all fractions will have the same denominator. So
I ask myself the question

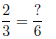
How do I figure out what the numerator should be ? I get an answer
of
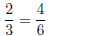(2)
Now, returning to problem of adding the two fractions given in (1),
we have

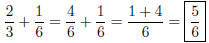
where I have replaced the fraction 2/3 with the equivalent fraction
4/6. Once this has been accomplished, the addition problem becomes
easy.

In this section, we concentrate on the skill of converting one fraction
into an equivalent fraction, this was the skill I used in (2) to
obtain a fraction with a denominator of 6.

2.1. A Short Lesson
Now, let’s discuss the strategy for writing equivalent fractions. There
are two basic methods that we use :
1. We can multiply both numerator and denominator by the same
number, and we will create a new fraction equivalent to the
original one;
2. we can divide both numerator and denominator by the same
number, and we will again create a new fraction equivalent to
the original one.

In this lesson, we will use method (1) to create equivalent fractions;
in the section on Reducing Fractions, we’ll use method (2).

Problem: Convert a fraction a/b
to an equivalent fraction having a
specified denominator, d. That is, write

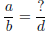
the problem is to figure out what the numerator is (the ‘?’).

To solve this kind of problem, most likely we multiply numerator
and denominator by some cleverly chosen number.

Example 1. Write the fraction 2/3
with a denominator of 6, that is,

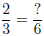
Solution: We ask ourself, 3 (the denominator we want to change)
times what number is equal to 6 (the denominator we want to change
to). The answer is 2 since 3 · 2 = 6. So. . .

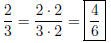
Rather than straining our brain looking for a number which multiplied
by 3 gives 6, we can simply divide. How many times does 3 go into 6,
that is 6/3= 2 and 2 is the number we are looking for.

Example 2. Write

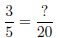
Solution: We ask ourself, 5 (the denominator we want to change)
times what number is equal to 20 (the denominator we want to change
to). The answer is 4 since 5 · 4 = 20. So. . .

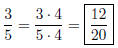
We could have computed 20/5 = 4 to get the 4 we need.

2.2. The Method
Before trying to do some problems on your own, let’s reduce our
method down to some simple steps .
Problem: Write .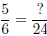
1. Divide the denominator 6 into the denominator 24: 24/6 = 4.
2. Multiply the numerator of the left-hand numerator by the number,
4, just computed in Step (1), to get the correct numerator
of the right-hand side:

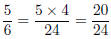
2.3. Some Quizzes
Test your understanding of the lesson by trying some of the quizzes
that follow. Begin by clicking on the “Begin” button. Enter your
answer where you see the question marks. When you are finished,
click on “End” button to see your how you did on the quiz. Click on
the “Correct” button to get the answers. Click on the “Ans” button
to see the correct answer; if this button has a green border, you can
shift-click to see a more detailed solution of this problem. If you jump
to a solutions, click on the green square to jump back to your quiz.

Convert the given fraction into one with the specified denominator.
Work in the margins or on scratch paper.


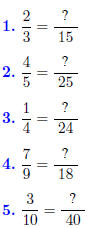
Answers:

Convert the given fraction into one with the specified denominator.
Work in the margins or on scratch paper.

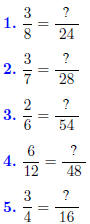
Answers:

Another, less important skill, is to write a fraction with a given
numerator equivalent to a given one. The method of solution is the
same, except we work with the numerator rather than the denominator.
Try these and see how you do.

Convert each fraction to the indicated equivalent fraction.


Answers:

3. Reducing Fractions
When presenting your final answer to an arithmetic problem, it is
important to reduce your answer to lowest terms. The process of
reducing a fraction to lowest terms is similar to converting a fraction
to an equivalent fractions; usually, we divide rather than multiply both
numerator and denominator by the same number to get the reduction.

We reduce a fraction by writing an equivalent fraction with a
smaller denominator. This is done by dividing the numerator and
denominator by the same number. For example,
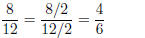(3)
Here, we have reduced 8/12, which has a denominator of 12, to an
equivalent fraction, 4/6, which has a denominator of 6. The denominator
has been reduced (in size).

Example 1. The fraction 2/3 is a reduced form of 4/6 since 4/6 = 2/3 and
the denominator of 2/3 smaller than the denominator of 4/6.

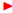A fraction a/b is reduced to lowest terms if it cannot be reduced.
In the case of Example 1, we reduced 4/6 to 2/3. This fraction, 2/3 , is
reduced to lowest terms, it cannot itself be reduced further.

Example 2. The fraction 12/18 can be reduced to 6/9, that is, 12/18 = 6/9 ,
but 6/9 itself can be reduced:

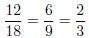
The reduced fraction 2/3 is reduced to lowest terms. This is the best
answer.

Now, how do we reduced fractions? Reduction is based on a simple
property of arithmetic :
1. If we multiply the numerator and denominator by the same number,
we do not change the value of the fraction.
2. If we divide the numerator and denominator by the same number,
we do not change the value of the fraction .
To reduce fractions, we use (2) above: divide numerator and denominator
by the same number.

Example 3. Express (reduce) the fraction 9/21 in lowest terms.
Solution: The strategy is to divide a the numerator and denominator
by the same number. Look at the given fractions 9/21 . We must think
of a number that divides both the numerator and denominator. (At
our level of play, look at some common values: 2, 3, 5)

After a few moments of meditation, we see that 3 divides numerator
and denominator of the given fraction. Thus,
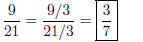(4)
To see if this is in lowest terms, we try again to find a number that
divides the numerator and denominator of our new fraction 3/7. We see
there is number that divides both numerator and denominator. So,
or, or answer in (4) is reduced.

Remember: Look at the given fraction, and try to think of a number
that divides both numerator and denominator. Once that is found,
divide!

Example 4. Express (reduce) the fraction 15/60 in lowest terms.
Solution: The strategy is to divide a the numerator and denominator
by the same number. Look at the given fractions 15/60 . We must think
of a number that divides both the numerator and denominator. (At
our level of play, look at some common values: 2, 3, 5)
The number 5 is an obvious choice,

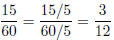
Is this expressed in lowest terms? No! We see that 3 divides both
numerator and denominator, so. . .
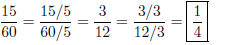(5)

Reduce each of the following fractions to lowest term.

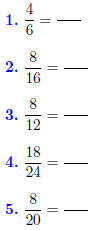
Answers:
That was so much fun, let’s try more of the same!

Reduce each of the following to lowest terms.

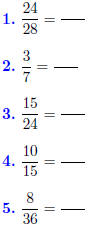
Answers:
Need more practice?

Reduce each of the following to lowest terms.

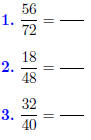
Answers:

All these problems are done the same way. Doing many problem
reenforces the technique. When you see a problem of this type in the
future, just apply these standard techniques!

Solutions to Quizzes

Solution to Quiz: We have 15/3 = 5, so we multiply the numerator
and denominator by 5.

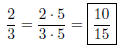
Solution to Quiz: We have 25/5 = 5, so multiply the numerator
and denominator by 5.

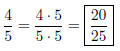
Solution to Quiz: We have 24/4 = 6, so we multiply the numerator
and denominator by 6.

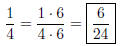
Solution to Quiz: We have 18/9 = 2, so we multiply the numerator
and denominator by 2.

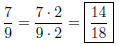
Solution to Quiz: We have 40/10 = 4, so we multiply the numerator
and denominator by 4.

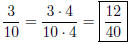
Solution to Quiz: We have 24/8 = 3, so we multiply the numerator
and denominator by 3.

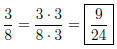
Solution to Quiz: We have 28/7 = 4, so we multiply the numerator
and denominator by 4.

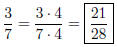
Solution to Quiz: We have 54/6 = 9 so we multiply the numerator
and denominator by 9.

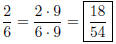
Solution to Quiz: We have 48/12 = 4 so we multiply the numerator
and denominator by 4.

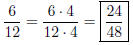
Solution to Quiz: We have 16/4 = 4 so we multiply the numerator
and denominator by 4.

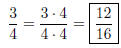
Solution to Quiz: Divide numerator and denominator by 8.

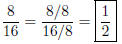
You could have also reduced in stages, first by 2, then 2 again, then 2 a
third. There are several other possible ways of reducing this fraction,
can you name one other way?

Solution to Quiz: Divide numerator and denominator by 4.

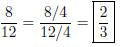
Solution to Quiz: Divide numerator and denominator by 6.

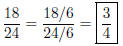
You could have also reduced in stages, first by 2, then by 3.

Solution to Quiz: Divide numerator and denominator by 4.

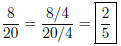
Solution to Quiz: Divide numerator and denominator by 4.

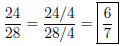
Solution to Quiz: This fraction is already reduced to lowest terms,
there is no number that divides both 3 and 7. The answer is

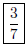
Solution to Quiz: Divide numerator and denominator by 3.

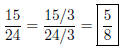
Solution to Quiz: Divide numerator and denominator by 5.

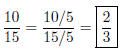
Solution to Quiz: Divide numerator and denominator by 4.

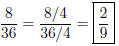
You could have also reduced in stages, first by 2, then by 3.

Solution to Quiz: Divide numerator and denominator by 8.

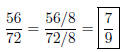
It may not have been obvious to divide by 8, but it would be obvious
to divide by 2

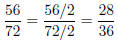
now by 2 again!

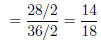
divide one more time by 2!!

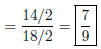
What we finally end up dividing by? We divided by 2, then 2 again,
finally by 2 a third time. In total, we divided by 2 · 2 · 2 = 8, which is
what we divided by in our first solution.

Solution to Quiz: Divide numerator and denominator by 6.

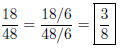
Solution to Quiz: Divide numerator and denominator by 8.