SOLVE THE EQUATION
x2 + 6x -7 = 0
Note: Equation must be in standard form, ax2 + bx + c = 0
1. BY FACTORING
2. BY COMPLETING THE SQUARE
| x2 + 6x − 7 = 0 |
To use this method the coefficient of x 2 must be
1. |
| x2 + 6x = 7 |
Rearrange the equation placing the constant on
the right-hand side. |
| x2 + 6x = 7 |
Find one-half of the coefficient of x and square
it (1/2 of 6 is3. 32 is 9.) |
| x2 + 6x + 9 = 7 + 9 |
Add the square to both sides. The resulting
trinomial on the left hand side of the equation is
a perfect square |
| (x + 3)2 = 16 |
[Note the perfect square is ( X + the ½ of the
coefficient of x from the step above)2] |
 |
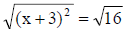Use the square root property on both sides of the
equation. |
| x + 3 = ± 4 |
Note: the resulting square root is both positive
and negative.[plus or minus] |
| x + 3 = 4 |
x + 3 = −4 |
Solve for both the positive and negative result. |
| x = 1 |
x = −7 |
|
3. BY USING THE QUADRATIC FORMULA
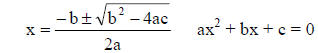
The formula is based on using the coefficients and
constant, a, b and c, from the standard form of the equation.
x2 + 6x − 7 = 0 a = 1 b = 6 c = −7 a is the coefficient of
x2, b is the coefficient of x, c is the constant.
Plug in the appropriate numbers . Note: If the work under
the square root sign , b2-4ac [the discriminant], is less than zero
[a negative number], then the equation has no real solution .
Solve for both the
positive and negative result.
Choosing a Method for Solving Quadratic Equations
• Simplify both sides of the equation and put it into
standard form, set equal to 0.
| x(x + 3) = 28 |
|
| x2 + 3x = 28 |
Distribute |
| x2 + 3x – 28 = 28 – 28 |
Subtract 28from both sides in order to set
equation equal to 0 |
| x2 + 3x – 28 = 0 |
Simplified, in standard form ,and set equal to 0.
Proceed to solve using method from other side of this handout |
• Factor out any common factors and divide both sides of
the equation by any common
numerical factor . This will eliminate it [zero divided by anything is zero]
| 2x2 – 8x – 10 = 0 |
|
| 2(x2 – 4x – 5 ) = 0 |
Factor out the common factor of 2. |
 |
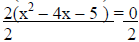Divide by 2 on both sides in order to eliminate
it . |
| x2 – 4x – 5 = 0 |
Factored, in standard form and set equal to 0. .
Proceed to solve using method from other side of this handout. |
• If no constant appears in the equation, then c = 0 and
there should be a common variable factor .
If so, use the factoring method.
| x2 – 4x = 0 |
|
| x(x – 4) = 0 |
Factor out the common x. |
 |
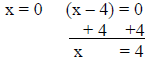Set each factor equal to 0.
Solve. |
 |
|
• If there is no first degree term [where there is no x
and therefore b = 0], use the square root
method:
| x2 - 4 = 0 |
|
 |
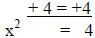Isolate the x2. |
 |
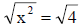Take square roots of each side of the equation. |
| x = ± 2 |
Solve. Remember: A square root always has a
positive and negative answer. |
