Vectors and Matrices II - Introduction to Matrices

Here we will continue our discussion of vectors and their transformations. In Lecture
6 we gained some facility with vectors (N-tuples) and we now want to discuss
generalized operations on vectors – a very common activity in physics. In particular
we will focus on linear functions of vectors, which are themselves sometimes vectors.
Consider first a general (scalar valued) function of a vector,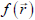 Recall that a
function is a linear function if, and only if, the following properties hold :

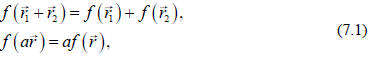
where a is a scalar (i.e., an ordinary constant). Examples of scalar valued functions
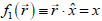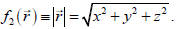of a vector are and Comparing to Eq.
(7.1) we see that  f₁ is a linear function and  f₂ is not! A similar definition of linearity
holds for vector valued functions of vectors as in the following

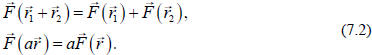
A trivial example of a linear vector valued function is 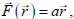multiplication by a
constant.

ASIDE: The definition of linearity in Eqs. (7.1) and (7.2) is the standard definition
for a linear operator 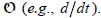In general we have

This line of reasoning (linear, vector valued functions of vectors) leads us directly to
the idea of matrices. As in Lecture 6 we want to connect the idea of vector valued
linear functions of general vectors to explicit (concrete) expressions for this operation
in terms of components defined by an explicit set of basis vectors,

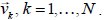
Expressing both 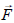and 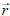in terms of components we have (introducing some
definitions; note we are assuming that 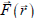and 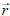are in the same vector space and
therefore can be expressed in terms of the same basis vectors)

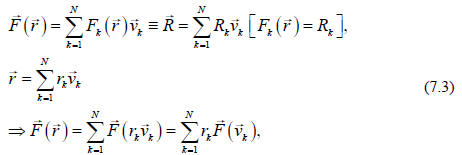
where the last step follows due to the linearity of 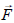Since 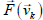is a vector, we
must be able to express it in terms of its components in the given basis set. Further
these components are important, and we should give them a name,

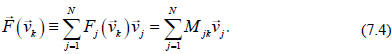
The NxN array of numbers 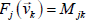(note the order of the indices ) is the matrix
mentioned earlier. Substituting back in Eq. (7.3) (and changing the order of the
sums) we have

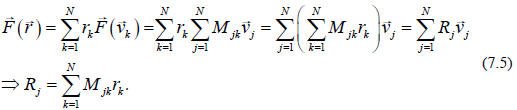
The last step follows from the uniqueness of the components, which is seen most
directly if we choose our basis vectors to be orthogonal (but this is not necessary).
We think of 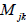as a square array of numbers where j defines the row and k the
column of a specific entry. Thus, given a specific basis set, a linear vector valued
function of vectors is defined by the corresponding matrix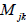 (just like a vector is
defined by its components in the chosen basis). If we think of the set of components
of a vector as a Nx1 matrix, then Eq. (7.5) illustrates matrix multiplication, the
elements in one row of the left-hand matrix times (one-at-a-time) the elements in a
column of the right-hand matrix. Looking back to Lecture 6 (recall Eqs.(6.12) and
(6.13)), we see that the scalar product of 2 vectors (in a Euclidean geometry) is just
the usual matrix multiplication of an 1xN matrix (the transpose of the vector) times an
Nx1 matrix,

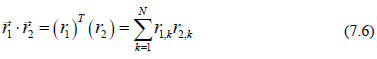
(or in the complex case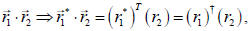 where the “dagger”
means the complex conjugate transpose, or Hermitian conjugate). We should also
note that Eq. (7.5) has the usual structure of simultaneous linear equations for N
unknowns in the case we know 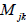and the 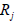and we want to solve for th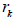e . We
will return to this subject in the next Lecture.

Clearly matrices are very useful in physics and we want to learn about their
properties, which will teach us about linear operators, simultaneous linear equations
and Group Theory (see Section 3.13). In the following discussion we will use capital
Roman letters to represent linear operators and their abstract matrices. Just as in our
discussion of vectors, we will be able to define “abstract” relations, independent of
any basis vector set, and concrete relations that involve the explicit components of
vectors and operators (matrices) with respect to specific basis vectors.

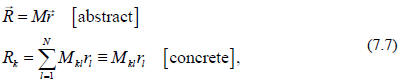
where in the very last expression we have employed the (standard) convention of
summing over repeated indices.

An interesting question is what kind of operations can we apply to the matrices
themselves? Clearly we can add (or subtract) matrices (i.e., add linear operators)

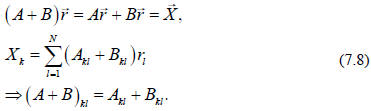
Adding matrices just means adding the corresponding elements. Addition of matrices
is associative and commutative

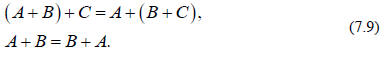
Also we can multiply matrices by constants (scalars), which is commutative,
associative and distributive,

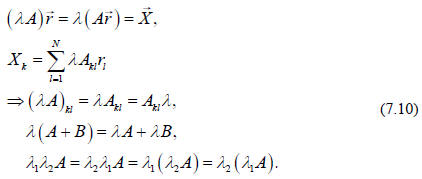
Finally we can define the multiplication of matrices, as we did earlier, as long as the
matrices are conformable, i.e., as long as the numbers of rows and columns match.
We will generally be considering square matrices, NxN, of the same dimension so
this point will not be an issue (i.e., our linear operation on a vector produces a vector
in the same vector space). We have

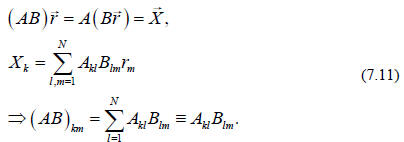
Matrix multiplication is associative, distributive, but not generally commutative (and
this last point is really important in physics),

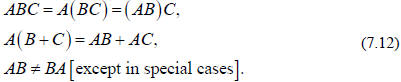
The difference implied by this last expression, AB - BA, is so important that we give
it a name, the commutator, and a symbol ( square brackets )

where the commutator has the form of another matrix C. (Note that the commutator
only makes sense when A and B are square matrices. Otherwise, even if AB and BA
both exist, they will be of different dimensions .) As we will see, the special case of
commuting matrices, 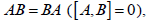also plays an important role in physics.
(Transformations associated with commuting matrices are called Abelian
transformations, while non-commuting transformations (matrices) are labeled non-
Abelian.)

To complete our introduction to matrices we need 2 special matrices (in analogy to
our discussion of vectors). The first is the null matrix (all elements zero)

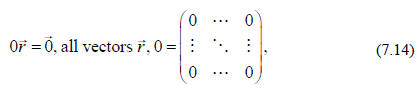
and the second is the unit matrix that we met first in Lecture 6,

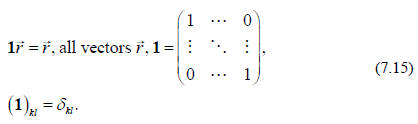
Note also that the equality of 2 matrices, A= B, means that 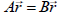for all 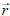. In
component notation two matrices are equal if, and only if, every element is identical,
.

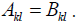While still focusing on square matrices, a special question (essential in the
application of matrices to simultaneous equations) is whether, given a matrix A, there
exists a second matrix, B, such that

i.e., we say that B is the inverse matrix to A. Further, if 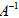exists, we say that A is a
non-singular matrix (see below). In operator language 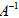represents the inverse of
the operation represented by A. For example, if A rotates vectors clockwise through
some angle about some axis, then 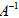rotates them counterclockwise through the
same size angle and about the same axis.

ASIDE: Even if the matrix A is not square but rectangular, 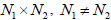, we
can still consider the question of finding an inverse, but in this case we must
distinguish the left-invers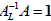e, , from the right-inverse, 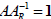, since
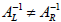(they necessarily have different dimensions if they exist, i.e., they satisfy
different conformality constraints and the 2 unit matrices in these equations have
different dimensions). This question will not be an issue in this course and we will
generally assume that only square matrices can be non-singular.

To be able to work with matrices it is useful to define 2 scalar quantities related to
each matrix A, i.e., these quantities characterize the matrix and are invariant under the
usual transformations of the matrix (i.e., scalar means invariant). They play a role
similar to that played by the length of a vector, 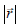. The first quantity is the trace of
the matrix written as

i.e., the trace is the sum of the diagonal elements. The second scalar quantity is the
determinant, which we already assumed in our discussion of the vector product of 2
vectors in Lecture 6. For a 2x2 matrix we have

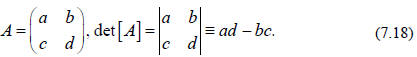
To analyze larger matrices we first define a couple more quantities. For the moment
just accept the following definitions. Their intrinsic value will become clear shortly.

Consider an NxN matrix A with elements 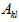. For specific values of the indices k and
l construct a new 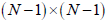 dimensional matrix by eliminating the 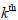row and
the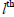 column. The determinant of this smaller matrix is called the “minor”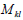 of
the original element 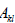. Since the minor yields a number for each value of k and l,
these numbers can be thought of as defining another NxN matrix. Next we multiply
the minor by a power of minus 1 defined by 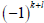and construct the so-called
“cofactor” 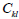of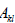 , which is itself an element of a NxN matrix,

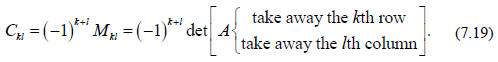
For example, as applied to a specific 3x3 matrix, we have

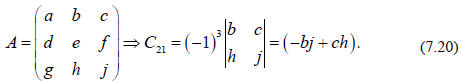
Now we can use the cofactors to connect 2x2 determinants (which we know from Eq.
(7.18)) to the desired NxN determinants. The general result is that we can evaluate
the determinant of an NxN matrix by first picking a specific (but arbitrary) row or
column, here we choose row k, and then evaluating the sum of each element in that
row times its cofactor,

where l is summed over and k is not. Since the cofactor itself involves a determinant
of a smaller matrix, we can iterate this expression in terms of determinants of
successively smaller matrices until we reach the 2x2 case (this construction is called
the Laplace development for determinants).

Square matrices with nonzero determinants are nonsingular matrices, and, as we will
see shortly, have inverses. If follows from this definition of the determinant
(although we will not go through the arithmetic here), that the determinant of a
product of matrices is the product of the individual determinants,

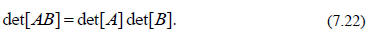
Consider some simple examples applying the rules above,

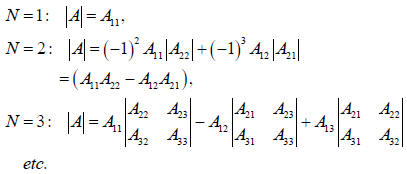
There are several important properties of determinants, following from Eq. (7.21),
that help to simplify the process of evaluating determinants (recall our motto).

1) If (all of the elements in) a single row or a single column are multiplied by a
constant c, the determinant of the new matrix is c times the determinant of the
original matrix.

2) The sign of a determinant (but not its absolute value) is changed if we interchange
2 rows or 2 columns.

3) The determinant is unchanged if we interchange all the columns with all the rows,
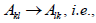the determinant of the transpose matrix is the same as the
determinant of the original matrix,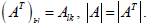

4) The determinant is unchanged if we add a constant times any row to another row,
or the same for columns.

5) The determinant of a matrix vanishes if all of the elements in any row or column
vanish.

6) The determinant of a matrix vanishes if any two rows or any two columns are
identical (as follows from points 4) and 5)).

7) The determinant of a matrix vanishes if any two rows or any two columns differ
by a constant multiplier, i.e., are proportional (as follows from points 4) and 5)).

We can use these properties to simplify a matrix, i.e., get as many zero elements as
possible, before taking the determinant (again, recall our motto!).

As an example consider the following matrix and evaluate its determinant by using
the elements in the first row

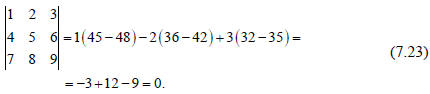
Instead consider proceeding by first subtracting 4 times the first row from the second
(R2-4*R1), then take 7 times the first row from the third row (R3-7*R1) and finally
subtract 2 times the second row from the third row (R3-2*R2)

We obtain the same answer but, in some sense, the arithmetic is simpler. Note that
this analysis also works the other way in the sense that for a vanishing determinant
we can always manipulate the form of the determinant, by using the rules above, into
an expression with all zeros along one row or one column.

To return to the question of finding the inverse of a matrix, consider a slightly edited
version of Eq. (7.21), i.e., consider what happens if we multiply a row (or column) of
elements by the cofactors of a different row (or column). For example, consider the
quantity, k ≠ m,

which we recognize as yielding the determinant of a matrix A' that differs from the
matrix A in that both the and the 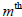row of A' are equal to the 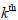row of A. Thus
these two rows in A' are equal to each other and by rule 6) above we can conclude
that det 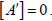The same is true for summing on the elements of a column. So the
right hand side of Eq. (7.25) can be nonzero only if (i.e., we only get a nonzero result
for the original expression for the determinant if) k = m,

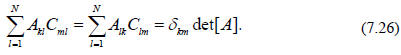
Recalling that the transpose of a matrix is obtained by exchanging rows and columns,

we are led to consider the product  AC^T  for which we can write, using Eq. (7.26), that

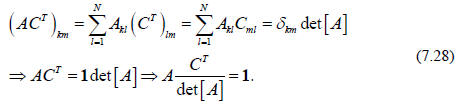
Comparing this last equation with Eq. (7.16) we see that we have found a general
expression for the inverse of the matrix A. We have

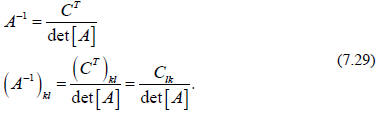
It should now be clear why nonsingular matrices with inverses require nonzero
determinants. The analogue statement to Eq. (7.22) about inverses of products is
(note the order of the matrices)

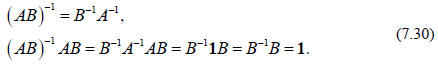
As an explicit example consider

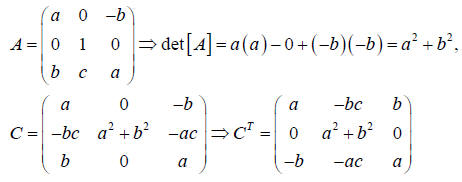
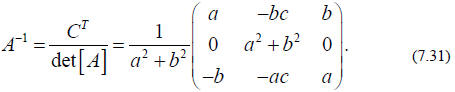
The reader is encouraged to verify that with the above expressions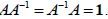

We close this introduction to/review of matrices with a summary of
vocabulary/notation and general properties.

Operations on matrices:

Transpose
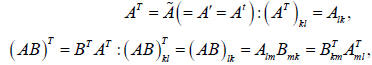Complex Conjugate
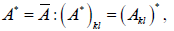Hermitian Conjugate [or Adjoint]
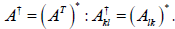Old Adjoint

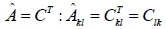Types of matrices:

Symmetric Matrix
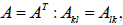Antisymmnetric Matrix
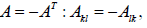Real Matrix
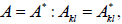Pure Imaginary Matrix
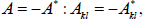Orthogonal Matrix
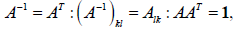Hermitian Matrix
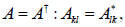Unitary Matrix
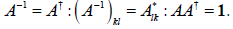