When adding or subtracting fractions we need both fractions to have the same
denominator. When this happens
we say that the fractions have Like Denominators . In order to keep our
computations to a minimum we will be
using the Least Common Denominator (LCD) as our like (or common) denominators.
There are three cases to consider:
♦Case 1: One denominator is a multiple of the other denominator.
♦Case 2: The two denominators are relatively prime ( equivalently , GCF = 1)
♦Case 3: The two denominators have a GCF ≠ 1.
Case 1: One denominator is a multiple of the other denominator.
Construction of the LCD : Use the larger of the two denominators as your LCD.
Examples:
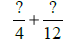 |
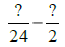 |
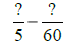 |
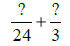 |
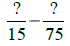 |
| 12 is a multiple of 4. |
24 is a multiple of 2. |
60 is a multiple of 5. |
24 is a multiple of 3. |
75 is a multiple of 15. |
| Use LCD = 12. |
Use LCD = 24. |
Use LCD = 60. |
Use LCD = 24. |
Use LCD = 75. |
Case 2: The two denominators are relatively prime
(equivalently, GCF = 1)
Construction of the LCD: Multiply the two denominators together to get your LCD.
Examples:
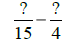 |
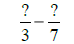 |
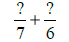 |
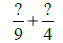 |
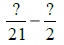 |
GCF(15, 4) = 1,
and 15 × 4 = 60. |
GCF(3, 7) = 1,
and 3 × 7 = 21. |
GCF(7, 6) = 1,
and 7 × 6 = 42. |
GCF(9, 4) = 1,
and 9 × 4 = 36. |
GCF(21, 2) = 1,
and 21 × 2 = 42. |
| Use LCD = 60. |
Use LCD = 21. |
Use LCD = 42. |
Use LCD = 36. |
Use LCD = 42. |
Case 3: The two denominators have a GCF other than 1.
Construction of the LCD: Use the prime factorization method (explained in class)
to construct the LCD.
Examples:
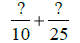 |
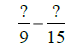 |
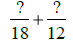 |
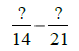 |
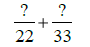 |
10 = 2 • 5 and
25 = 52 , so the
LCD = 2•52 |
9 = 32 and
15 = 3• 5, so the
LCD = 32 •5 |
18 = 2 •32 and
12 = 22 •3 , so the
LCD = 22•32 |
14 = 2•7 and
21 = 3 •7, so the
LCD = 2 •3• 7 |
22 = 2• 11 and
33 = 3• 11, so the
LCD = 2 •3• 11 |
| Use LCD = 50. |
Use LCD = 45. |
Use LCD = 36. |
Use LCD = 42. |
Use LCD = 66. |
Practice Identifying the
Least Common Denominator (LCD)
The Least Common Denominator (LCD) is the Least Common Multiple ( LCM ) of the
denominators.
In cases 1 and 2, the LCD, if computed, would be the simpler forms described in
the handout. Case 3 is the
only case that actually requires an official computation for the LCD.
From before:
♦Case 1:
One denominator is a multiple of the other denominator.
1. Use the larger of the two denominators as your LCD.
♦Case 2:
The two denominators are relatively prime (equivalently, GCF = 1)
1. Multiply the two denominators together to get your LCD.
♦Case 3:
The two denominators have a GCF ≠ 1.
1. Use the Prime Factorization Method to construct the LCD.
Indicate the cases to which the denominators belong. Then, indicate the LCD.
•Do your scratch work for Case 3 on another sheet of paper.
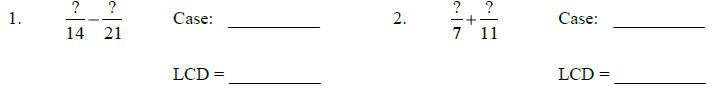
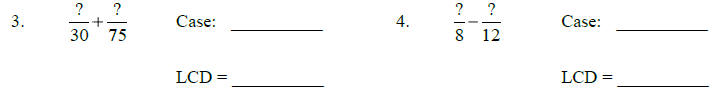
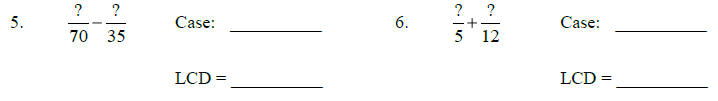
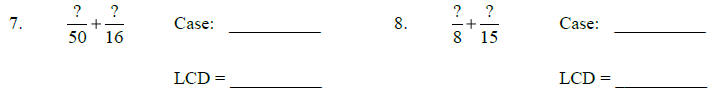
Solutions :
1.) Case 3; LCD = 42 2.) Case 2; LCD = 77 3.) Case 3; LCD
= 150 4.) Case 3; LCD = 24
5.) Case 1; LCD = 70 6.) Case 2; LCD = 60 7.) Case 3; LCD = 400 8.) Case 2; LCD
= 120



