If y = f(x) and y = g(x) are polynomials , then it follows
from a theorem in algebra that
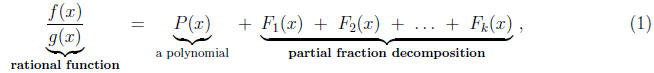
where each partial fraction Fi has one of the forms
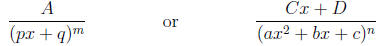
where
•
m and n are nonnegative integers, i.e.,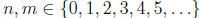 
•
ax2 + bx + c is irreducible, i.e., it cannot be factored over R, i.e. b2 - 4ac
< 0 .
Why do we care? Well, if (1) holds then
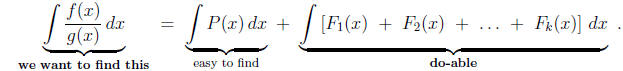
So how to find this decomposition ....
| First Case: [degree of y = f(x)] < [degree of y =
g(x)] |
In this case, P(x) = 0 in (1). Express y = g(x) as a
product of
•
linear factors px + q
•
irreducible quadratic factors ax2 + bx + c (irreducible means that b2 - 4ac <
0).
Collect up the repeated factors so that g(x) is a product of different factors of
the form (px + q)m
and (ax2 + bx + c)n. Then apply the following rules.
Rule 1: For each factor of the form (px+q)m where m ≥ 1, the decomposition (1)
contains a sum
of m partial factions of the form
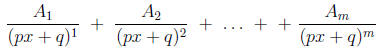
where each Ai is a real number.
Rule 2: For each factor of the form (ax2 + bx + c)n where n ≥ 1 and b2 - 4ac < 0,
the decomposi-
tion (1) contains a sum of n partial factions of the form
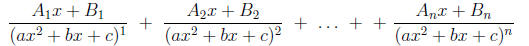
where the Ai's and Bi's are real number.
| Second Case: [degree of y = f(x)] [degree of y =
g(x)] |
First do long division to express
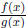as
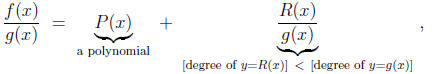
How to do this? Well we surely see that
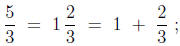
we get this by long division
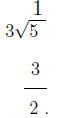
Similarly,
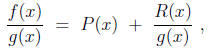
where
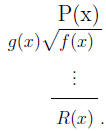
Now we can apply the First Case to
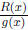since [degree of y = R(x)] < [degree of y =
g(x)].
A common mistake . Note that x2 = (x - 0)2 = 1x2 + 0x + 0
and so b2 - 4ac = 0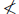 
0. So we follow
Rule 1 to see that the partial fraction decomposition of
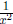is of the form
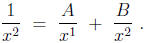
Note that A = 0 and B = 1. A common mistake is to try to
use Rule 2, which would give
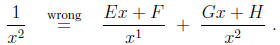
This would still lead to the correct answer (E = F = G = 0
and H = 1) but you have to do LOTS
of work to get to it.
