Directions: Follow all directions carefully. Show all work
(where applicable). Problems without work may
not receive full credit. The quadratic formula is something that you will need
to have memorized. For now,
I will give it to you but will not tell you how to use it. The quadratic formula
is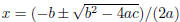 
.
In problem 1 (a) label the sides that run parallel to the tight rope as x. The
total number of points on this
quiz is 25.
1. Recall that the area of a trapezoid is given by
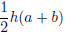where h is the height of the trapezoid, and
a
and b are the lengths of the parallel sides. A hexagon-shaped circus tent has a
60 foot long tight rope
from one of the corners to another, cutting the tent into two equally -sized
trapezoids. The rope is 20 feet
from the outer edges of the tent (to allow the tight rope walker enough room to
have his long balance
stick). The area of the tent floor is 2000 square feet . Do the following:
(a) (2 points) Draw the tent as viewed from above with the tight rope and any
lengths given in the
problem properly labeled. Bring this drawing up to me so I can verify it is
correct.
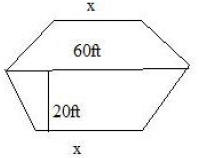
The biggest mistake here was not following the directions
and labeling the sides x.
(b) (4 points) Find the length of the two sides of the tent parallel to the
tight rope.
Notice that the entire area of the tent floor is 2000 square feet , so the area
of each trapezoid is
1000 square feet (since the tight rope cuts the tent into two equally sized
trapezoids). So we have
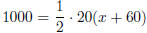, 10x + 600 = 1000, 10x = 400 and x = 40, so
the length of each side of the
tent parellel to the tight rope is 40 feet.
(c) (4 points) Suppose all of the circus' elephants take up 35 square feet when
viewed from above.
Assuming the malleability of the elephants, how many could be placed on the
floor of the tent?
There is an implied "each" in this sentence. If you were unclear about this you
should have asked
me for clarification. So if each elephant takes up 35 square feet and we have
2000 square feet to
work with, then we set 35y = 2000 and get y ≈ 57.14 so we can get 57
elephants in the tent.
(d) Solve the following linear equations.
(a) (2 points) 17y + 12 = -3y + 4
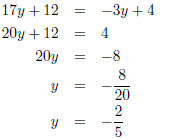
(b) (3 points)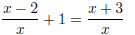 
First we should note that x ≠ 0. However since there were only 3 points to give
here, I decided
not to take o for failure to note that.
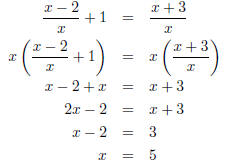
Double checking our answer we get
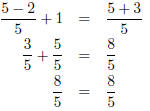
So x = 5 is a solution.
(c) Perform the indicated operations involving complex numbers and write the
result in standard form.
(a) (2 points) (7 + i)(15 - 2i) Here we foil.
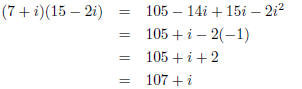
(b) (3 points)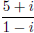 
Here we
must multiply by one in a clever way. We use the complex conjugate
1 + i over itself.
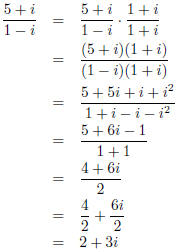
(c) Given the following quadratic equation x 2 +
8x + 15 = 0 do the following:
(a) (1 point) Find the discriminant of the quadratic.
The discriminant of a quadratic equation is the b 2 - 4ac part of the
quadratic equation. Here
we have a = 1, b = 8, c = 15 so we look at 82 - 4(1)(15) = 64 - 60 =
4. So the discriminant of
this quadratic is 4.
(b) (1 point) What does the discriminant tell you about the solutions to the
quadratic equation?
Here, a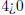s 
, we know that we will get two
(distinct) real solutions .
(c) (3 points) Solve the quadratic equation. This could be done in two ways. I
will outline each
as subparts.
(a) We can factor the left hand side of this equation.
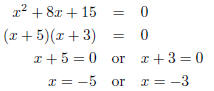
(b) We could use the quadratic equation. In this case
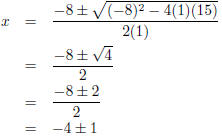
So x = -4 - 1 = 5 or x = -4 + 1 = -3.
