Polynomial and Synthetic Division

I. Long Division of Polynomials
We use long division to find factors of a polynomial.
For f (x) = 6x³ −19x² +16x − 4 if you look at the graph
one x- intercept is x = 2 therefore x = 2 is a zero and
(x - 2) is a factor of f(x). This means there is some 2^nd
degree polynomial q(x) such that
f (x) = (x − 2) • q(x)

We can use long division to find q (x).There is no remainder
Ex: Divide x²– 3x+ 5 by x +1.
Tip: Remember to subtract every term

The Division Algorithm.
For all polynomials f(x) and d(x) such that d(x) ≠ 0 and
the degree of d is less than or equal to the degree of f,
there exist unique polynomials q(x) and r(x) such that
f(x) = d(x)q(x) + r(x)
divided = divisor • quotient + remainder

where r(x) = 0 or the degree of r is less than the degree of d.
If the remainder r(x) is zero , d(x) divides evenly into f(x)
We can also write the division algorithm


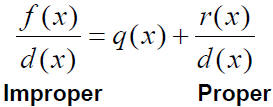
Before you apply Division Algorithm
1. Write the dividend and divisor in descending powers
of the variable
2. Insert placeholders with zero coefficients for missing
powers .

Ex: Divide x³-1 by x – 1.

II. Synthetic Division
Short cut for long division
Divide ax³ + bx² + cx + d by x − k
1. List the coefficients of the dividend inside the bracket
2. Place k outside the bracket
3. Vertical pattern: Add terms
4. Diagonal pattern: Multiply by k
5. Result gives you the coefficients of the quotient and

the remainder which is a constant
The previous procedure applies only when the divisor is
of the form x – k, and when every descending power of x
has a place in the dividend.

Ex: Use synthetic division to divide 4x⁴- 2x²– x + 1 by x + 2.

III. The Remainder and Factor Theorems
The Remainder Theorem
If a polynomial f(x) is divided by x – k, the remainder r
is r = f(k). A proof is given on page 192 of the text.
Synthetic division can be used to evaluate a function at x = k
Ex: Use the Remainder Theorem to find f (-2) for
f (x) = 3x³ + 8x² + 5x − 7

The Factor Theorem
A polynomial f(x) has a factor x – k, if and only if f(k) = 0.
A proof of the Factor Theorem is given on page 192 of the text.

Use synthetic division and the remainder theorem to
apply the factor theorem

Ex: Show that x – 1 is a factor of f(x) = x⁴- 1.
Ex: Show that (x – 2) and (x – 3) are factors of
f (x) = 2x ⁴+ 7x ³− 4x ²− 27x −18

Uses of the Remainder Theorem and Synthetic Division
The remainder r obtained in the synthetic division of f(x)
by x – k provides the following info:
1. The remainder r gives the value of f (x) at x = k that is
r = f(k).
2. If r = 0, (x – k) is a factor of f(x) .
3. If r = 0, ( k , 0 ) is an x - intercept of the graph of f(x)