Problems for Math Solutions

This department welcomes problems believed to be new and at a level appropriate for the readers
of this journal. Old problems displaying novel and elegant methods of solution are also invited.
Proposals should be accompanied by solutions if available and by any information that will assist
the editor. An asterisk (*) preceding a problem number indicates that the proposer did not submit a
solution.

All correspondence should be addressed to Harold Reiter, Department of Mathematics, University
of North Carolina Charlotte, 9201 University City Boulevard, Charlotte,  Electronic submissions using LATEX are encouraged. Other
electronic submissions are also encouraged. Please submit each proposal and solution preferably
typed or clearly written on a separate sheet (one side only) properly identified with name, affiliation,
and address. Solutions to problems in this issue should be mailed to arrive by March 1, 2008.
Solutions identified as by students are given preference.

Problems for Solution.

1146. Proposed by Douglas Shafer, University of North Carolina Charlotte This
problem first appeared here in fall 2006. It has not yet been solved successfully .
Because of a contribution from Professor Ali Amir-Moez, we are able to offer a $500
prize for the best undergraduate student solution to this problem.

Given six real constants a, b, c, d, e, and f, not all zero , a conic section C :
ax² + bxy + cy² + dx + ey + f = 0 is determined. Since rescaling the six coefficients
by a nonzero number does not change C , we may view (a, b, c, d, e, f) as lying in
S⁵ ⊂ R⁶. If (a, b, c, d, e, f) is selected based on a uniform distribution on S⁵, what is
the probability that C is an ellipse ?

1159. Proposed by S.C. Locke, Florida Atlantic University, Boca Raton, FL
Suppose that

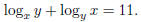
Evaluate

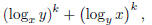
for k = 2, 3, 4, 5.

1160. Proposed by Leo Schneider, John Carroll University, University Heights,
OH

Construct a proof that e is an irrational number based on the Alternating Series
Test.

1161. Proposed by Jos´e Luis D´ıaz-Barrero, Universidad Polit´ecnica de Catalu˜na,
Barcelona, Spain.

Find all continuous functions f : R → R such that

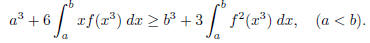
1162. Proposed by Paul S. Bruckman, Sointula, BC
Given 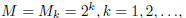prove the congruence

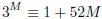(mod 64M), for k ≥ 3.

Also, prove the ”near” corollaries:
1. 3^M 1 + 20M(mod 32M), for k ≥ 2.
2. 3^M 1 + 4M(mod 16M), for k ≥ 1.
3. 4M || (3^M −1), for k ≥ 1; that is, the largest exponent t such that 2^t divides
(3^M − 1) is t = k + 2.

1163. Proposed by Stas Molchanov, University of North Carolina Charlotte

A two-pan balance and 16 coins of different weights are given. What is the fewest
number of usages of the balance needed to determine the heaviest coin, the second
heaviest coin, and the third heaviest coin?

1164. Proposed by Cecil Rousseau, University of Memphis
Find a formula for evaluating the trigonometric sum

cos²ⁿ 1° + cos²ⁿ 2° + · · · + cos²ⁿ 89° ,

where n is a positive integer . Your formula should demonstrate that each such sum
is a rational number . For example,

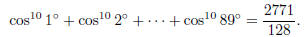
1165. Proposed by Marcin Kuczma, University of Warsaw, Warsaw, Poland

For positive integers n, k let F(n, k) be the number of mappings of an n-element
set into itself whose k^th iterate is the identity map (e.g. F(3, 2) = 4 ) – and let the
number F(4, 2) + F(8, 2) + F(8, 3) be nice and lucky and happy for you!! Editor’s
note: this puzzle was sent to friends of the poser in December of a certain year as a
gift. This is the seventh of several such problems we plan for this column.

1166. Proposed by Peter A. Lindstrom, Batavia, NY

Suppose that functions f, g, f', and g' are continuous over [0, 1] , g (x) ≠ 0 for
x 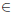[0, 1] , f (0) = 0, g (0) = π, f (1) = 1004, and g (1) = 1. Find the value of

1167. Proposed by Richard Armstrong, St. Louis Community College and Arthur
Holshouser, Charlotte, NC

Find necessary and sufficient conditions on positive integers a, b, c, and d such
that

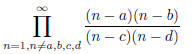
converges.

1168. Proposed by Sam Vandervelde, St. Lawrence University , Canton, NY
Define the Fibonacci numbers as usual by
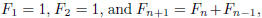
for n ≥ 2. Determine the value of

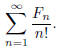
1169. Proposed by James A. Sellers, Pennsylvania State University, University
Park, PA

A composition of the positive integer n is an ordered sequence of positive integers
which sum to n . So, for example, 3 + 4 + 2, 4 + 3 + 2, and 2 + 2 + 2 + 3 are different
compositions of the number 9. Let c_o(n) be the number of compositions of n where
the last part is odd.
1. Find a Fibonacci-like recurrence satisfied by c_o(n).
2. Use the above recurrence to find a closed formula for c_o(n).

1170. Proposed by Andy Niedermaier, University of California San Diego

Consider a 10 × 10 grid of lights, each either on or off, which we denote using
matrix notation 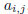, where, for each i = 1, 2, . . . , 10 and j = 1, 2, . . . , 10, the entry in
row i and column j is 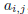and its value is 0 or 1. We are allowed two types of moves.
For each 1≤ u ≤ 8 and 1 ≤ v ≤ 8, we can change the status of all the lights for
which both u ≤ i ≤ u + 2 and v ≤ j ≤ v + 2. This is called a small block move. The
other type move is, for each 1 ≤ u ≤ 6 and 1 ≤ v ≤ 6, we can change the status of all
the lights 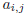for which both u ≤ i ≤ u + 4 and v ≤ j ≤ v + 4. This is called a large
block move. So essentially, we can change the status of all nine lights in each 3 × 3
subarray and of all the lights in each 5 × 5 subarray. Is it possible, beginning with
the all on configuration, to achieve all possible on-off configurations of lights?