Graphing the Conic Sections

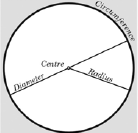
Now we are ready to begin graphing circles . Recall from geometry that the
radius of a circle is one -half of its diameter or d = 2r. Also, it will be useful to
know that the perimeter of a circle, or circumference, is given by C=2πr
and the area is given by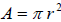

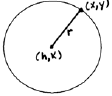
Equation of a Circle - (standard form)

where r is the radius and (h, k) is the center.

From the equation of a circle in standard form we can see that a circle is
completely determined by its center and radius. In addition , notice that it is
not a function because it fails the vertical line test .

Graph
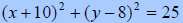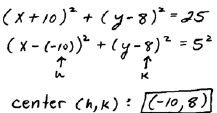
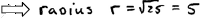		First plot the center . Then use the radius and plot points 5 units up, down, left and right. Label the points on the circle.
Use standard form to identify the radius r and the center (h, k).

Even though a circle is not a function, it is a relation and we could still find the domain
and range. In addition, we will be asked to find the x- and y-intercepts. This particular
example does not have any but the technique to find them is the same method used
throughout this study guide.

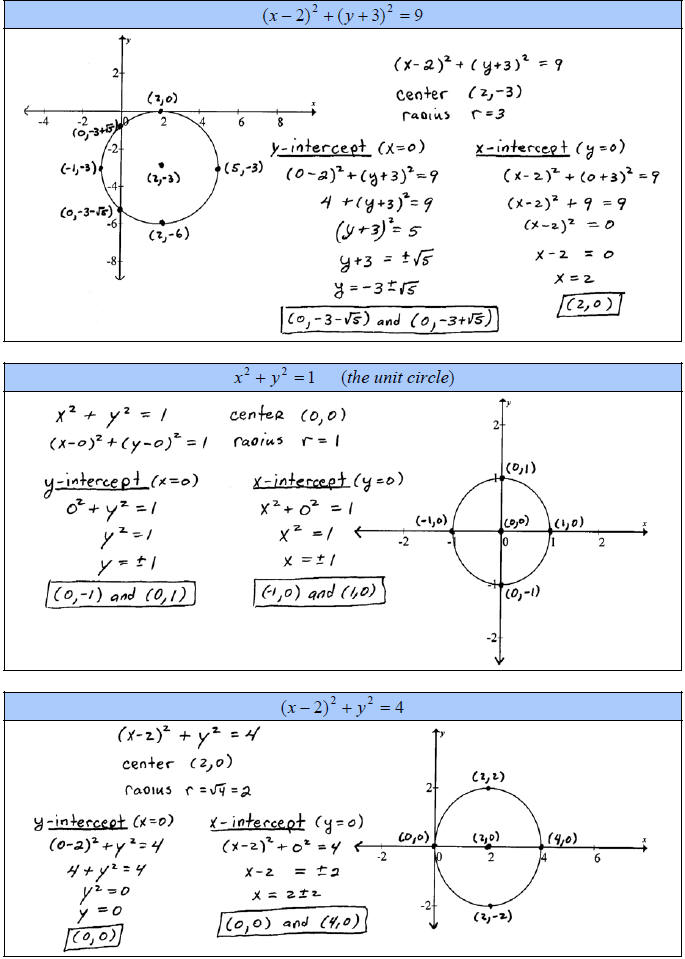
To find y- intercepts set x=0 and solve for y.
To find x-intercepts set y=0 and solve for x .

A. Graph the circles and label the x- and y-intercepts.

Graphing circles in standard form is just a matter of identifying the center and the radius.
The difficulty comes when the circle is not given in standard form. In this case we will
have to complete the square twice as illustrated below.

	Rewrite in standard form
Group all terms with variable x and group all terms with variable y.		Add or subtract the constant term to the other side.
Complete the squares .		Then add to both sides of the equation for each variable grouping .

B. Rewrite the circles in standard form and identify the center.

C. Find the area of the following circles.

Graph , find the x- and y-intercepts, area, and circumference
D. Find the equation of the circle with:
Center (-1, 5) and radius 7 units	Center (0, -3) and diameter 20 units