Graphs and Equations
Start by making statements such as the following: Graphs provide a means
of displaying, in-
terpreting, and analyzing data in a visual format. Many real -world situations
can be described
mathematically using equations in two variables . Each pair of variables
represents a solution to
the equation and can be displayed as a single point, or ordered pair (x, y), on
a coordinate plane.
The coordinate plane is devised of two perpendicular lines called the
which divide
the plane into four regions, called 
. The
horizontal line is called the
and the vertical line is called the 
.
Plot points : At this point, I would ask students
how to describe how to plot a point or two, which
quadrant the point lies in, etc.
Solutions of Equations: How many different ways
can you show, or prove, that a pair is a
solution? The relationship among ordered pairs , solutions to equations, and
points on a graph is
essential.
Determine whether each ordered pair is a solution of 2x + 3y = 18.
(a) (-5, 7)
(b) (3, 4)
(c) If (4,A) is on the graph of 2x - 5y = 8, find A. This is a typical
homework/test question.
Graphs of Equations:
To graph an equation is to make a drawing that represents the
of that equation.
Students should be able to graph by plotting points, key points are the
intercepts.
An x- intercept is a point (a, 0). To nd a,
.
The x-intercept is also called a zero because 
A y-intercept is a point (0, b). to nd b,
.
Examples: Graph by nding intercepts.
2x + 3y = 18
3x - 5y = -10
Graph y = x2-9x-12 by plotting points. [Create a table of points by using a
graphing calculator.]
Distance This is one of the last topics in Math
002 and should be familiar to students.
The distance d(P1, P2) between two points P1(x1, y1) and P2(x2, y2) is
given by
Use the distance formula to verify that (-6, 3), (3,-5),
and (-1, 5) form a right triangle. .. or
some other example where the students need to show they know how to use the
distance formula.
Find all points having an x-coordinate of 4 whose distance
from (-3,-1) is 13. This can be done
by the distance formula and/or by plotting points and reasoning through the
Pythagorean Theorem.
Start by making a sketch, then ask for suggestions.
Midpoint Midpoint is pretty intuitive , although
students may later confuse the formula with the
formula for slope .
The coordinates of the midpoint of a line segment with endpoints (x1, y1) and
(x2, y2) is given by
Example: Find the midpoint of the hypotenuse in the right
triangle above. Extra. Use if time and
if the above example was used.
Circles Circles will be new to Math 002
students. Many have not had a geometry course for several
years. Connect to the distance formula.
De nition: A circle is the set of all points that are
from a given point. The
given point is 
. The constant distance is
called the 
.
The general form for the equation of a circle is:
The standard form for the equation of a circle is:
where
is the
and 
is the
.
1. Identify the center and radius for the circle given by
(x - 1)2 + (y - 5)2 = 4.
2. Write the equation for the circle with center at
and radius
. Sketch the graph.
Do variations of this question with center on an axis, in di erent quadrants,
etc. and radii
that are integers as well as simple radicals , like
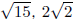and so on.
3. Find the center and radius of the circle given by x2 +
y2 - 6x - 4y - 4 = 0. completing the
square is a familiar , but not necessarily pro cient, skill for Math 002
students.
4. What is the center of the circle with diameter
endpoints at (-2, 5) and (4,-3)? Write the
equation of this circle.
