Definition of a Quadratic
Inequality
A quadratic inequality is any inequality that
can be put in one of the forms
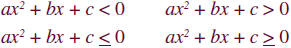
where a, b, and c are real numbers and a = 0.
Procedure for Solving Quadratic Inequalities
• Express the inequality in the standard form
• 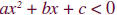 or
or 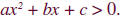
• Solve the equation 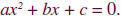 The real solutions are
the
The real solutions are
the
boundary points.
• Locate these boundary points on a number line, thereby
dividing the number line into test intervals.
• Choose one representative number within each test interval. If
substituting that value into the original inequality produces a
true statement, then all real numbers in the test interval belong
to the solution set. If substituting that value into the original
inequality produces a false statement, then no real numbers in
the test interval belong to the solution set.
• Write the solution set; the interval(s) that produced a true
statement.
Example
Solution
Step 1 Write the inequality in standard form. We can write by
subtracting 2 from both sides to get zero on the right.
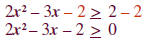
Step 2 Solve the related quadratic equation. Replace the
inequality
sign with an equal sign. Thus, we will solve.
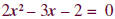 |
This is the related quadratic equation. |
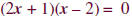 |
Factor. |
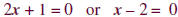 |
Set each factor equal to 0. |
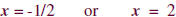 |
Solve for x. |
The boundary points are –1/2 and 2.
Solve and graph the solution set on a real number line:
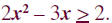
Solution
Step 3 Locate the boundary points on a number line. The
number line with the boundary points is shown as follows:

The boundary points divide the number line into three test
intervals. Including the boundary points (because of the given
greater than or equal to sign), the intervals are (-∞, -1/2], [-1/2, 2],
[2, -∞).
Solve and graph the solution set on a real number line:
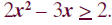
Solution
Step 4 Take one representative number within each test interval and
substitute that number into the original inequality.
| Test Interval |
Representative
Test Interval Number |
Substitute into
2xΔ – 3x ≥ 2 |
Conclusion |
| (-∞, -1/2] |
-1 |
2(-1)2 – 3(-1)≥ 2
5 ≥ 2, True |
(-∞, -1/2] belongs |
| [-1/2, 2] |
0 |
2(0) 2 – 3(0) ≥ 2
0 ≥ 2, False |
[-1/2, 2] does not
belong to the
solution set. |
| [2, ∞) |
3 |
2(3)2 – 3(3)≥2
9 ≥ 2, True |
[2, ∞) belongs to
the solution set. |
Solve and graph the solution set on a real number line:
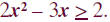
Solution
Step 5 The solution set are the intervals that produced a true
statement. Our analysis shows that the solution set is
(-∞, -1/2] or [2, ∞).
The graph of the solution set on a number line is shown as follows:

Text Example
Solve and graph the solution set: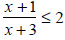
Solution
Step 1 Express the inequality so that one side is zero and the other
side is a single quotient. We subtract 2 from both sides to obtain zero on
the
right.
Solve and graph the solution set
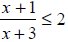
Solution
Step 2 Find boundary points by setting the numerator and the
denominator equal to zero.
The boundary points are -5 and -3.Because equality is
included in the given
less-than-or-equal-to symbol, we include the value of x that causes the
quotient to be zero. Thus, -5 is included in the solution set. By contrast, we
do not include 1 in the solution set because -3 makes the denominator x-14+
zero.
Solve and graph the solution set: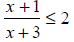
Step 3 Locate boundary points on a number line.
The boundary points divide the number line into three test intervals, namely
(-∞, -5],[-5,-3),(-3,∞).
Solve and graph the solution set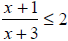
Step 4 Take one representative number within each test
interval and
substitute that number into the original equality.
Test
Interval |
Representative
Number |
Substitute into
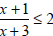 |
Conclusion |
| (-∞, -5] |
0 |
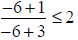 True True |
(-∞, -5]does belong to the
solution set. |
| [-5,-3) |
2 |
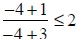 False False |
[-5,-3)does not to the
solution set. |
| (-3,∞) |
5 |
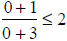 True True |
(-3,∞) does belong to the
solution set. |
Solve and graph the solution set: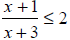
Step 5 The solution set are the intervals that produced
a true
statement. Our analysis shows that the solution set is (-∞, -5]
or (-3,∞)
The Position Formula for a Free -Falling
Object Near Earth’s Surface
An object that is falling or vertically projected into
the air has its height in feet above the ground
given by
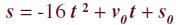
where s is the height in feet, v0 is the original
velocity (initial velocity) of the object in feet per
second, t is the time that the object is in motion in
seconds, and s0 is the original height (initial
height) of the object in feet.
Example
An object is propelled straight up from ground level with
an initial velocity of
80 fps. Its height at time t is described by 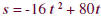 t where the height, s,
t where the height, s,
is measured in feet and the time, t, is measured in seconds. In which time
interval will the object be more than 64 feet above the ground?
Solution
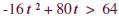 |
This is the inequality implied by the problem’s
question. We must find t. |
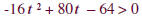 |
Subtract 64 from both sides. |
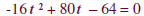 |
Solve the related quadratic equation. |
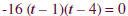 |
Factor. |
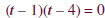 |
Divide each side by 16. |
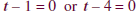 |
Set each factor equal to 0. |
 |
Solve for t. The boundary points are 1 and 4. |
An object is propelled straight up from ground level with
an initial velocity of
80 fps. Its height at time t is described by s = -16t Δ + 80 t where the height,
s, is measured in feet and the time, t, is measured in seconds. In which time
interval will the object be more than 64 feet above the ground?
Solution
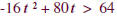 |
This is the inequality implied by the problem’s
question. We must find t. |
 |
The boundary points are 1 and 4.
Since neither boundary point satisfy the
inequality, 1 and 4 are not part of the solution. |

With test intervals (-∞, 1), (1, 4), and (4, ∞), we could
use 0, 2, and 5 as test
points for our analysis.
An object is propelled straight up from ground level with
an initial velocity of
80 fps. Its height at time t is described by 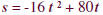 t
where the height, s,
t
where the height, s,
is measured in feet and the time, t, is measured in seconds. In which time
interval will the object be more than 64 feet above the ground?
Solution
Test
Interval |
Representative
Number |
Substitute into
(x – 1)(x – 4) < 0 |
Conclusion |
| (-∞, 1 |
0 |
(0 – 1)(0 – 4) < 0
4 < 0, False |
(-∞, 1) does not belong to |
| (1, 4) |
2 |
(2 – 1)(2 – 4) < 0
-2< 0, True |
(1, 4) belongs to the
solution set. |
| (4, ∞) |
5 |
(5 – 1)(5 – 4) < 0
4 < 0, False |
(4, ∞) does not belong to
the solution set. |
The object will be above 64 feet between 1 and 4 seconds.



