Problems likely to be quizzed on and/or graded for the
next assignment:
4.1
8, 12, 18, 24
4.2
10, 12, 32, 44, 54, 64 (don't be afraid of word problems)
This is NOT a guarantee that only these problems will be quizzed/graded, just
that
they are likely.
Solutions to Homework #4
3.3.6
Use the given zero(s) of f to factor f (x), and then find the remaining zeros.
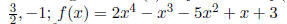
Since 3/2 and -1 are factors of f(x), that means it is
possible to write f(x) in the following
way:
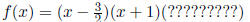
Where the (??????????) is simply what is leftover when we
factor our the first two terms.
LOOK: If you plug in x = 3/2 , then we get the following:
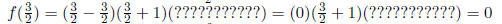
That is what it means for 3/2 to be a zero for f (x). You
plug in that number, and the
whole function goes to zero. Clearly, the same thing happens if we plug in -1.
We have those zeros already though. What we want are the
zeros of the (?????????),
which means we have to find out what (?????????) is. To do that, we use division
to divide
out the terms we already know exist. You can use long division with the (x- 3/2
) and (x+1),
or you can use synthetic division with the zeros themselves.
Let's divide using synthetic division first. Fortunately, as
long as you don't make any
arithmetic mistakes, doing division with 3/2 is relatively painless.
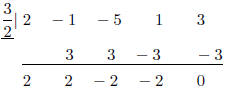
You just bring down the first coefficient (number in front
of the x4), and multiply that
by the value you are evaluating at (which is 3/2 in our case), write the result
in the next
column and add vertically . Then repeat.
As expected (and required), we get 0 in the last column,
which indicates our remainder is
0. IF YOU DIDN'T GET ZERO, THAT MEANS YOU MADE A MISTAKE AND NEED
TO CHECK YOUR ARITHMETIC. It does NOT mean you just leave it and go onto the
next problem.
Now, we have completed the synthetic division using our
first zero, and so this informa-
tion tells us that we can write f(x) as:
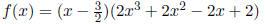
Okay, part of the way there. Now do synthetic division
with -1 on WHAT IS LEFT-
OVER. Don't go back and try to divide the original function again. What do we
gain?
Nothing! We want the original function factored by BOTH the zero terms we were
given.
So, here we go:
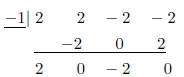
This means we can write our function as:
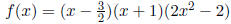
We now know what the (????????) is from earlier! That was
the whole point of what
we did. (In case you haven't figured it out yet, understanding what you are doing
and why
you are doing it is the key to being good at math.)
So now we can find the zeros of our last factor, by setting
it equal to zero and solving
for x.
2x2 - 2 = 0
2x2 = 2
x2 = 1
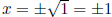
Therefore are remaining roots are x = 1 and x = -1. We
already had x = -1 as a root
given to us, so that means that x = -1 is a double root.
Therefore, the zeros of our function are:
x = 3/2 , x = 1, x = -1 (double root)
3.3.28
Use the given zero of f to factor f(x), and then find the remaining zeros.
i; f(x) = x3 + 2x2 + x + 3
This problem has the same instructions as the previous one , it just involves a
complex
term. Don't let it scare you. Just look closely to see how I do the synthetic
division.
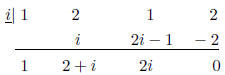
Just remember to only add like terms, and that i2 = -1,
and you'll be all set.
Now, we've factored out (x - i), and so our f(x) looks something like:
f(x) = (x - 1)(x2 + [2 + i]x + 2i)
Which is painful to look at. So, let's factor that last
little bit using our knowledge of
the fact that complex roots ALWAYS come in conjugate pairs, provided the coefficients
of
the polynomial we are using are all real (and they are, since there are no i's
in the original
function.)
So, let's factor out that (x + i) by using -i in our synthetic division.
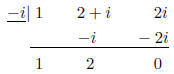
Therefore:
f(x) = (x - i)(x + i)(x + 2)
This tells us that our zeros are:
x = i, x = -i, and x = -2.
3.4.4
Use the Rational Zero Theorem to list all the possible rational zeros of the
function. Use
synthetic division and/or a graphing calculator to help you determine which are
actually
zeros.
h(x) = x4 - 17x2 + 16
Mind your p's and q's now. List all the factors of the
constant term, 16, and then list
all the factors of the leading coefficient, which is 1.
p :± 1,±2,±
4, ±8, ±16
q :± 1
Therefore all rational zeros are of the form p/q, where p
and q come from the lists we
just made:
possible rational zeros: ±1,± 2,±4,±
8, ±16
Clearly, since all our q's are just 1, our list of
rational zeros is the same as our list of
p's.
Now, do like I did, and just plug that equation into your
graphing calculator and you'll
quickly see that it LOOKS like ±1 and ±4
are your roots. You should use the 2nd CAL-
CULATE function on your graphing calculator (if you have a TI-83 or 84) to
verify those
are the roots. Or, even simpler, just look at the table. Start the table at -4,
move in
increments of 1 and verify that you get 0 for the output at -4, -1, 1, and 4.
Synthetic division works too. In fact, if you need
practice with synthetic division, I
suggest using this problem to practice. We KNOW -4, -1, 1, and 4 will cleanly
factor our
function that we were given, so you have a good set of numbers to practice with.
Be careful,
and make sure you write the function as f(x) = x4 + 0x3 - 17x2 + 0x + 16,
otherwise your
columns will get all screwed up.
3.5.2
Find the domain and the zeros of the rational function and match it with its
graph.
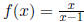
First up, fond the domain. Since many people seem to
actually not understand what the
domain IS, let me define it in simple terms:
The DOMAIN is all the x values that you can put into the
function, and that will give
you an output.
Since it is impossible to divide by zero, then FINDING
when the denominator is zero
will tell us what x CAN'T be. Clearly, x = 1 will make the denominator zero, and
so:
D : x ≠ 1
Or 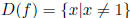
Or domain: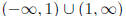
All are acceptable answers for the domain. Do me a favor though and LABEL your
answers. Many people had "answers" all over the place, but didn't indicate what
was a
zero, what was the domain, what was, whatever. In mathematics you must
communicate
clearly, so if multiple things are asked for, make sure to indicate what is
what.
Ok, moving on.
Now let's find the zeros. To do that, just set the top equal to zero and solve for
x .
x = 0
Boy, that was hard. x = 0 is our zero. That means the
point (0; 0) is on our graph.
That's the origin, so any graph you make MUST have the function passing through
the
origin of the graph.
Let's go figure out what graph it is now.
From our research into the domain, we know that the
denominator equals zero when
x = 1, so there should be a vertical asymptote at x = 1. Two graphs on page 282
satisfy
this property, graph i and graph v. However, only graph v passes through the
origin, and
so that is our graph.
3.5.22
Find all vertical and horizontal asymptotes and sketch the graph.
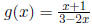
Vertical asymptotes are easy. Find when the denominator is
zero:
3 - 2x = 0
-2x = +3
x = 3/2
That is our vertical asymptote.
Finding our horizontal asymptote is a little bit harder. To find that, select
the highest
power of x anywhere in the function, and divide EVERY term in both the top and
the
bottom by that power of x.
In our case, the highest power is simply x. So now divide:
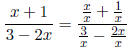
Simplify by canceling x's.
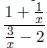
Now, as x goes to 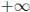 or
or
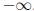 then everything with an x under it goes to
zero. So we
then everything with an x under it goes to
zero. So we
end up with:
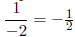
Or, more precisely:
g(x) = -1/2
Yes, horizontal asymptotes are described by OUTPUT values. DO NOT put x = -1/2 ,
because that is not true! It is y = -1/2 (or g(x) = -1/2 ).
If you want to see a graph of the function, just plug it
into your graphing calculator and
graph. Use almost any of the default windows they give you to get a good view.



