§5.9 The Slope of Quadratic Functions
When an object is dropped (in a vacuum and over a short distance) the
distance travelled after t seconds is given by the function:
d(t) = 16t2.
How fast is this object travelling after 2 seconds? In other words what is
the slope of the graph of this function at t = 2?
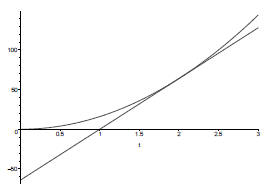
Clearly the slope is different depending on where on the graph we wish to
compute the slope. The diagram shows the tangent line at the point (2, 64).
But we only have one point to work with, so we cannot compute the equation
of the tangent line, nor its slope.
What we can do is approximate the tangent line by picking two points
on our graph and computing the slope of the line between them.
Lets compute the slope of the line through the points (2, f(2)) and (3, f(3)).
f(2) = 16 · 22 = 64 and f(3) = 16 · 33 = 144
We have
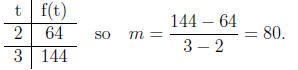
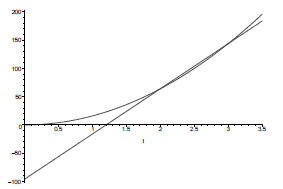
We can see that the line with slope 80 passing through (2, 64) is not the
tangent line, and does not have the correct slope, but we can find better
approximations by picking our second point closer to (2, 64). So lets pick our
second point to be (2.5, f(2.5).
f(2.5) = 16 · (2.5)2 = 100
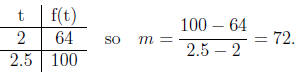
We could continue to pick values closer to 2, and each would be a better
approximation. To get the exact answer seems to be an impossible task, but
in the 17th century the Mathematician and Physicist , Sir Isaac Newton had
an idea. Instead of picking the second point before you calculate the slope ,
pick the second point after you compute the slope. The way he did that
was to pick the second time to be an increment h bigger than the first thus
the second point would be (2+h, f(2+h) The value h would be determined
after we do our computations. In our example we have
f(2 + h) = 16 · (2 + h)2 = 16(4 + 4h + h2) = 64 + 64h + 16h2.
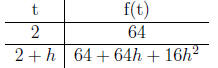
so
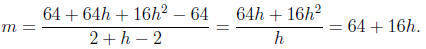
Now we are free to chose h as small as we like to get the two points close
together and get the best approximation. But Wait! we might as well pick
h so small that it might as well be zero so we write
64 + 16h → 64
And we have rounded off our approximate answer to an exact answer.
And we conclude that the object is travelling at 64 feet per second after 2
seconds.
Example An object launched upward at a velocity v0 from a height s0 will
be
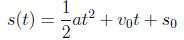
above the ground after
t seconds, where 
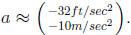
a represents the acceleration of gravity and it is negative since the accel-
eration is down, and the distance is measured up.
Assume the initial velocity, v0, is 15 m/sec and the initial height, s0 is
20m, then our height function is
s(t) = −5t2 + 15t + 20.
1. How high does it fly?
2. When does it hit the ground?
3. How fast does it hit the ground?
4. How fast is it travelling when it reaches its maximum height?
Solutions
1. To find how high it flies we find the vertex of the parabola .
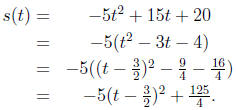
So after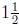 
seconds the
object reaches a maximum height of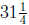 
meters.
2. To find when it hits the ground we must find the zeros of the functions .
s(t) = −5t2 + 15t + 20 = 0
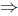−5(t2 − 3t − 4) = 0
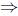−5(t − 4)(t + 1) = 0
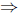t = −1 or t = 4.
Since we are looking into the future (and not the past), we conclude
that the ball hits the ground after 4 seconds.
3. To find the speed at which the object strikes the ground, we find the
velocity at the time it hits the ground, which we have just calculated
to be 4 seconds.
We know that s(4) = 0 so we compute
s(4 + h) = −5(4 + h)2 + 15(4 + h) + 20 =
−5(16 + 8h + h2) + 60 + 15h + 20 = −25h − 5h2.
So we have
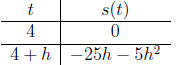
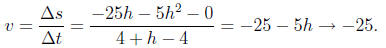
So the object strikes the ground with velocity 25 meters per second in
a downward direction.
4. To find the velocity of the object at its maximum height we compute
its velocity at the time it is at its maximum height which we know to
be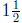 
seconds. We also know that height to be
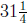meters, so we must
compute the height at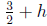 
seconds.
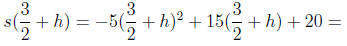
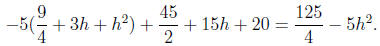
So we have
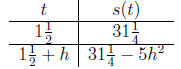
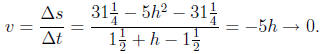
So we conclude the object has 0 velocity at its maximum height. But
this should be obvious to us, since it has stopped going up and is about
to start going down.
