Math 310 Midterm

(1a) Use the mathematical induction to show that for all n ∈N,

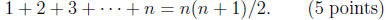
(1b) Use (n + 1)^3 - n^3 = 3n^2 + 3n + 1 and (1a) to show

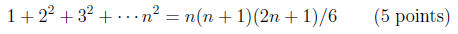
(1c) Use the method in (1b) to find

(Renark: Of course, (1a) can also be done by the method of (1b) by
quoting the identity (n + 1)^2 - n^2 = 2n + 1. However, you must use
the mathematical induction to solve (1a).)

(2a) Use the Euclidean division algorithm to show that for any two
natural numbers m and n , there is a natural number q such that mq >
n. (10 points)
(Hint: Divide n by m .)

(2b) Conclude that for any two positive rational numbers r and s, there
is a natural number n such that nr > s. (5 points)

(Remark: (2b) is the reason why you can pick the first natural number
N≥a given positive rational number , say, 10/ε , in all of our ε-N
proofs.)

(3) Show that the definition of the product of two real numbers is
well-de fined independent of the representatives chosen. (10 points)

(4a) Let I_n = {k ∈N : k ≤n}. Suppose f : I_n -> N is a one-to-one
function, that is f(x) = f(y) implies x = y. Let I_m(f) be the image of
f in N. Use the mathematical induction to show that there is another
one-to-one function g : I_n -> I_m(f) such that g is an onto map, that
is, each element in I_m(f) is the image of some element in I_n via g, and
moreover g(x) < g(y) if x < y. (10 points)

(Remark: In spite of its dry statement, the problem simply says
we can reshuffle the image elements so that the new map is order-
preserving . For instance, if

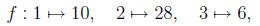
then

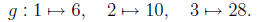
Here, I_n = {1, 2, 3} and I_m(f) ={6, 10, 28}.

(4b) Conclude that if m < n then a function f : I_n -> I_m cannot be
one-to-one. (5 points)

(Remark: This is the Pigeon Hole Principle that says that if the
number of pigeons is greater than the number of pigeon holes, then
there must be a pigeon hole with at least two pigeons .)

(5) Show that between any two real numbers x and y satisfying x+1 <
y, there is an interger n such that x < n < y. (10 points)

(Hint: Without loss of generality, we may assume 0≤x≤y (why?).
Consider the nonempty set of natural numbers ≥ y (why is this set
nonempty?). Apply the well- ordering principle to this set.)

(6) Show that nⁿ/n! is not Cauchy. (10 points)