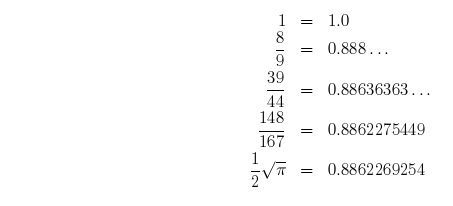Early in the study of the history of mathematics , we come across various
rational approx -
imations to irrational numbers. What I mean by that is that when what we know to
be
an irrational number was used in a computation, a rational number was used
instead. A
well known example of this is Archimedes’ approximation
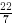of the irrational number π. Of
course, 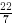is not exactly equal to π, but it’s
pretty close .
The question is, how did Archimedes ever come up with this approximation? The
answer
is known how Archimedes and the Greeks before him found these approximations,
but you
may not have seen it before. It’s sometimes called antenaresis or the method of
continued
fractions , and it’s related to Euclid’s algorithm for finding the greatest
common divisor .
Long before Archimedes, others used rational approximations in Egypt, Babylonia,
India,
and China. They may have used the same method, but in those cases, there is no
record of
the method. There are other methods that have been used in specific instances,
but when
you see a denominator , like 7, that has nothing to do with the numerical
base—usually 10,
sometimes 60—that’s a good indication that antenaresis was used.
sometimes 60—that’s a good indication that antenaresis was used.
What is this method? Let’s take an example to see how it goes. Suppose we’re
trying
to “ square the circle ,” that is, find a square whose area equals the area of a
given circle.
The ratio of the side of the resulting square to the diameter of the original
circle will be an
irrational number, so an approximation will have to be used in computations.
We’ve seen that the Egyptians used the square on
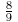of the diameter, and a different
approximation was used in India, so this particular problem was an important one
for thee
ancients.
First of all, some geometric method is required to give some kind of numerial
approxima-
tion, then the antenaresis method will give a nice rational approximation that
can be used in
practice. Let’s suppose that somehow we’ve discovered a good decimal
approximation . Since
we know the area of a circle to be πr2, therefore the side s of an equal square
will be
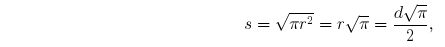
so the ratio of the side s of the square to the diameter d
of the circle will be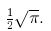
That
means, a good decimal approximation will be 0.886227.
Now, the question is, what’s a good rational approximation
to 0.886227?
Well, the first approximation, which isn’t very good, is the nearest integer,
namely 1.
That’s not a very good approximation since it approximates the circle by the
circumscribed
square, which is much too big. We want a better approximation.
How far off is our first approximation? Well, 1 - 0.886227
equals 0.113773. Can we
approximate 0.113773 with a nice rational number? It’s about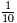 
,or
is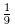 
a better approxima-
tion? Here’s the trick. Reciprocate that number. We get 1/0.113773 = 8.789432.
Since 8.7
is closest to the integer 9, that means 0.113773 can be pretty well approximated
by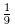Now
we have our second approximation: 0.886227, which is 1-0.886227 can be
approximated by
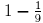, which is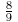That’s
the ancient Egyptian approximation.
Does this mean that the Egyptians used antenaresis? Not
necessarily, but at least it ’s a
possibility.
How do we get the next approximation? Let’s look at the error we got with the
last
approximation. We approximated 8.789432 by 9, which was too large by 0.210568.
Use the
reciprocation trick again. We get 1/0.210568 = 4.790597, which is pretty close
to 5. So a
better approximation than for 8.789432 is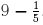
That
means a better approximation than
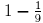for 0.886227 is
There is no known ancient instance of using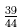
for
approximating this ratio.
This method works for better and better rational approximations, so long as you
have
good data going into it. If you don’t have a very good approximation to begin
with, then
only the first couple of stages of antenaresis are useful. The number of stages
you use should
depend on the degree of accuracy of your approximation.
If you’re interested in approximating this particular ratio, here’s a comparison
table for
the first few stages.
